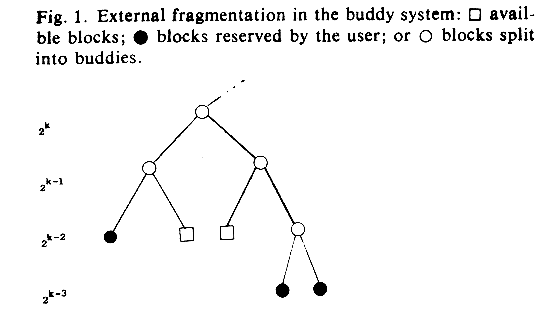
Figure 1. External fragmentation in the buddy system.
| Home | Up | Questions? |
Copyright © 1974 by the Association for Computing Machinery, Inc. Permission to make digital or hard copies of part or all of this work for personal or classroom use is granted without fee provided that copies are not made or distributed for profit or commercial advantage and that copies bear this notice and the full citation on the first page. Copyrights for components of this work owned by others than ACM must be honored. Abstracting with credit is permitted. To copy otherwise, to republish, to post on servers, or to redistribute to lists, requires prior specific permission and/or a fee. Request permissions from Publications Dept, ACM Inc., fax +1 (212) 869-0481, or permissions@acm.org.
ACM did not prepare this copy and
does not guarantee that is it an accurate
copy of the author's original work.
An extension of the buddy method, called the weighted buddy method, for dynamic storage allocation is presented. The weighted buddy method allows block sizes of 2k and 3*2k, whereas the original buddy method allowed only block sizes of 2k. This extension is achieved at an additional cost of only two bits per block.
Simulation results are presented which compare this method with
the buddy method. These results indicate that, for a uniform
request distribution, the buddy system has less total memory
fragmentation than the weighted buddy algorithm. However, the
total fragmentation is smaller for the weighted buddy method when
the requests are for exponentially distributed block sizes.
CR Categories: 3.89, 4.32, 4.39
Keywords and Phrases: weighted buddy algorithm, buddy system, memory
allocation, dynamic storage allocation
The buddy system [2, 3] is an algorithm for dynamic storage allocation. It provides storage in block sizes which are powers of 2, from a pool of available memory space of size 2m. An available space list keeps track of available blocks. When a block of size 2k is requested, the available space list is examined. If a block of the proper size is available, it is used. Otherwise, an iterative request for a block of size 2k+1 is made. This block, when obtained, is split into two blocks, called buddies, both of size 2k. One block is placed on the available space list, and the other is used to fill the request. When a block is released, its buddy is examined. If both buddies are free, they are combined to recreate the block from which they were created. If the buddy of this resulting larger block is free, then it is also combined with its buddy. This process repeats until no further combination is possible. The resulting block is placed on the available space list.
Two aspects of the algorithm are important: its execution speed and its effectiveness in storage utilization. The running time of the buddy system is determined by the number of blocks which are split and combined. The effectiveness of the algorithm in managing memory can be determined by measuring two types of losses in storage utilization: internal memory fragmentation and external memory fragmentation [5]. Internal fragmentation is the result of allocating only blocks of predetermined sizes, so that a request for memory must be rounded up to the next larger block size.
External fragmentation is the result of breaking down memory into separate blocks which cannot be combined into a desired larger block. External fragmentation can occur in the buddy system because two empty blocks of size 2k cannot be used to fill requests for blocks of size 2k+1 unless they are buddies. This situation is illustrated in Figure 1. Knuth [3] has shown by simulation that external fragmentation is not significant for the buddy method. Purdom and Stigler [4] have shown similar results using a stochastic model of the buddy system. Internal fragmentation, however, is a major problem. Knuth has shown that there may be a loss of between one-fourth and one-third of memory due to internal fragmentation.

Figure 1. External fragmentation in the buddy system.
The weighted buddy system decreases the amount of internal fragmentation by allowing more block sizes. Blocks may be of sizes 2k, 0 ≤ k ≤ m, and 3*2k, 0 ≤ k ≤ m - 2. With this scheme, allowed block sizes are 1, 2, 3, 4, 6, 8, 12, ... . In the weighted buddy system there are nearly twice as many block sizes as are available in a standard buddy system. The reduction in internal fragmentation is achieved at a cost of two extra bits of "overhead" in each block and a slight increase in running time, relative to the buddy method.
A related algorithm for dynamic storage allocation has been considered by Hirschberg [1]. That algorithm allocates memory in block sizes which are Fibonacci numbers.
Section 2 of this paper discusses the weighted buddy method. Section 3 describes results of simulating the algorithm.
The weighted buddy method is similar to the original buddy method in that large blocks are split iteratively to provide the desired smaller blocks; and when blocks are released, they are combined with their buddy if the buddy is available, or, failing this, are attached to an available space list. Other similarities are: (1) the ease of calculating the address of the buddy of a block, given the block's address; and (2) the allocation of blocks from an available space list.
The differences between the two methods lie in how the blocks are split, the mechanism of address calculation, and other more minor variations arising from a wider choice of block sizes.
As in the buddy method, the total memory consists of 2m words addressed for convenience from 0 through 2m-1. This memory forms the first block. The blocks are split in two different ways depending on the size of the block to be split. This is illustrated in Figure 2. A block of size 2k+2 is split into two blocks of sizes 3*2k and 2k. Blocks of size 3*2k are split into sizes 2k+1 and 2k. Blocks split from the same parent block are called buddies. Since the buddies of a pair have different sizes, they are called weighted buddies. We shall simply call them buddies where there is no ambiguity. Note that, in any split, the larger of the two resulting buddies always has a size which is the next smaller block size of the block sizes generated by the weighted buddy system.
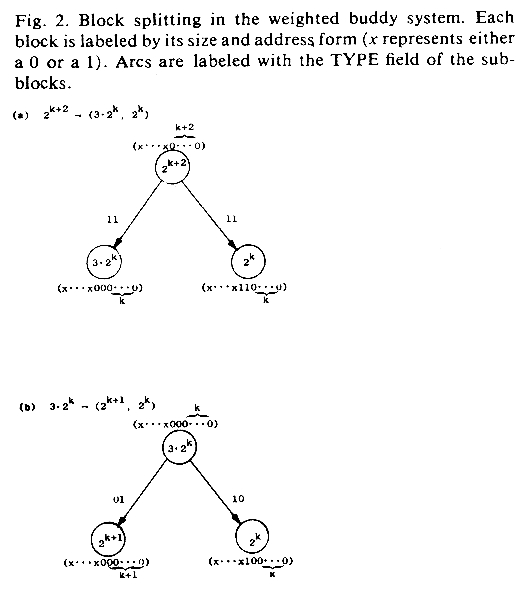
Figure 2. Block splitting in the weighted buddy system. Each block is labeled by its size and address form (x represents either a 0 or a 1). Arcs are labeled with the TYPE field of the subblocks.
Example. Figure 3 gives an example of a tree for the weighted buddy method when all possible splits have been made. In this example, we have an original memory block of 32 words.
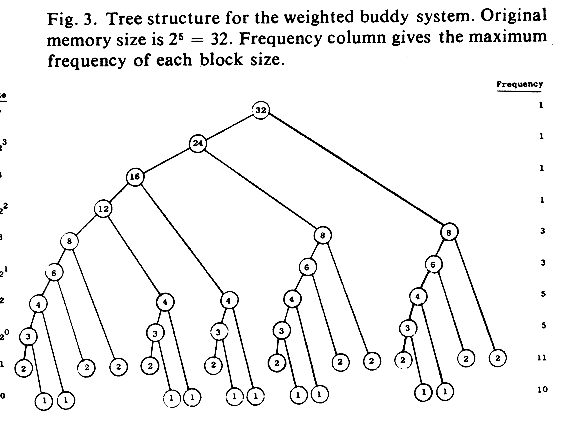
Figure 3. Tree structure for the weighted buddy system. Original memory size is 25 = 32. Frequency column gives the maximum frequency of each block size.
An available space list (ASL) keeps track of all available blocks of storage. The ASL consists of 2m doubly linked table locations, AVAIL(2m), ..., AVAIL(1), serving as the heads and tails of linked lists of available storage of sizes 2m, 3*2m-2, 2m-1, ..., 3, 2, 1, respectively. Available blocks have two link fields, forward and back- ward links, which link the blocks to the appropriate element of the ASL. Initially, there is only one block of size 2m attached to the ASL at the top. As requests for blocks arrive, this large block is split. In general, any element of the ASL may have several blocks of the same size attached to it as a doubly linked list.
New available blocks are attached to the end of this linked list, and blocks desired for satisfying requests are removed from the front of the appropriate list as in a queue. A queue is used instead of a stack because of the simulation results which are discussed later. When a block is released and its buddy is available, then the buddy is removed from the ASL for recombination and the recombined block is placed on the ASL. The ASL uses a doubly linked list to facilitate the block removal for recombination.
When a block of size 2k is desired but not available, the following method is used to determine how a larger block is to be repeatedly split until a block of size 2k is generated.
Given a request for an unavailable block of size 2k, we search Up the ASL Until we reach the first available block of size greater than 2k. This block is removed from the ASL, and split into two blocks. We continue splitting the smallest subblock greater than or equal to the requested size until the requested block size is matched. The same procedure holds if the request is for a block of size 3*2k.
Owing to the manner in which blocks are split, the form of the address for the buddies (i.e. the address of its first word) has the following property.
THEOREM. The address of a block of size 2k is a multiple of 2k (i.e. the address in binary notation has at least k zeros on the right). The address of a block of size 3 * 2k is a multiple of 2k+2.
PROOF. We prove this result by induction on k with k = m, m - 1, ..., 0. For k = m, we assume without loss of generality that the largest block of size 2m has a starting address of zero [3]. As illustrated in Figure 2(a), this block is split into buddies, and the 3*2m-2 sized block will have a starting address of zero, while the 2m-2 sized block will have a starting address of 3*2m-2.
We next assume the form to be true for all blocks of size 2k+2. As illustrated in Figure 2(a), it is also true for all blocks of size 3*2k and 2k. This is because the address for the 3 * 2k size block is the same as that of the parent 2k+2 block, and the address for the 2k size block comes from adding the value 3*2k in binary to the address of the block of size 3*2k. As illustrated in Figure 2(b), the resulting 3*2k sized block is used as the new parent block for splitting. The form is now similarly preserved for all blocks of size 2k+1 and 2k owing to the address form for the 3*2k sized block. Therefore, the form holds for all blocks of size 2k, and 3*2k.
A corollary of this theorem is that the address of any block of size 2k which is the "right-handed" split from a 2k+2 sized block (Figure 2a), has a binary form of x...x110...0 with exactly k zeros on the right. The 2k sized block which is a right-handed split from a 3*2k sized block (Figure 2(b)) has a binary form of x...x100...0 with exactly k + 1 zeros on the right.
To distinguish between these different kinds of splits, a two-bit TYPE field (not in the original buddy method) is used in every block:
| TYPE(P) | = | 11 if the block with address P is split from a 2k size block, |
| = | 01 if the block with address P is the left split from a 3*2k block, | |
| = | 10 if the block with address P is the right split from a 3*2k block. |
We now show how to find the address of the buddy of a block, given the size and address of the block. Let WBk(x) be the address of the (weighted) buddy of a block of size c*2k and address x, where c is 1 or 3. (The address, x, and the type field associated with the block at x, denoted by TYPE(x), contain sufficient information to determine c. Therefore, c is omitted from the notation, WBk(x).) We define WBk(x) by:
| WBk(x) | = | x + 3*2k if x mod 2k+2 = 0 and TYPE(x) = 11, |
| = | x - 3*2k if x mod 2k+2 = 3*2k and TYPE(x) = 11, | |
| = | x + 2k if TYPE(x) = 01, | |
| = | x - 2k+1 if TYPE(x) = 10. |
Besides the overhead of maintaining the ASL, a one-bit TAG, field is needed to indicate the available/reserved status of the block. Also, a KVAL field is needed to indicate the value of k. If the block is of size c*2k, only k need be remembered. These fields are also needed for the standard buddy system, so the only additional space overhead for the weighted buddy system is the two-bit TYPE field.
We denote the maximum possible frequency of occurrence of each block size in the weighted buddy method by F(i), where i = 1, 2, ..., 2*m is an index for each distinct size. This frequency may be found by solving the following recurrence relations.
| F(i) | = | F(i + 1), for i odd, 3 ≤ i ≤ 2*m |
| F(i) | = | F(i + 1) + F(i + 3) + F(i + 4), for i even, 2 ≤ i ≤ 2*m - 4, |
| F(1) | = | F(3) + F(4), |
| F(2*m) | = | F(2*m - 2) = 1. |
For the block size of 2k, k = 1, 2, ..., m, and the block size of 3*2k-2, k = 2, 3, ..., m, the solution of the above equations gives a frequency of occurrence equal to 1/3*(2m-k+1 + (-1)m-k).
The basic simulation program to compare the buddy and the weighted buddy methods of dynamic storage follows the outline given in Knuth [3]. We repeat the method below.
Let TIME be initially zero and all of memory initially be available.
Detailed statistics on parameters such as internal fragmentation and other steady state characteristics were printed whenever TIME was a multiple of 200. The steady 561 state was reached for values of TIME larger than about 2000. Two block size distributions for S were used in the experiments:
The time distribution was a random integer chosen uniformly between 1 and 100 for both block size distributions. Since both S1 and S2 limit block sizes requested to between 100 and 2000, the two buddy algorithms were limited to allocating blocks of size between 128 and 2048. The total memory size assumed available was 217.
The memory wasted for each allocated block is the difference between the size of the allocated block and the size of the request. The sum of this memory waste over all allocated blocks is the internal fragmentation.
Memory overflow occurs when a request for memory cannot be satisfied because only smaller blocks are available. When overflow occurs, the ratio of the amount of unallocated memory to the total memory size is the external fragmentation. To measure external fragmentation, memory overflow was activated by ceasing to release blocks after a given time (2000 for our simulations).
When a steady state is reached, the average number of blocks which must be split into buddies to satisfy a request and the average number of blocks which are recombined with their buddies when a block is released are equal. The average number of splits and recombinations for the weighted buddy method was 0.66 in our simulation as compared to 0.20 for the buddy method. Since the running time of these algorithms is proportional to the number of splits and recombinations needed, the weighted buddy method will increase the running time overhead by approximately a factor of three. It should be remembered that this increase in execution time is for only the request and release mechanisms, which will probably take only a small portion of the time for the overall computing task.
Uniform (S1) Exponential (S2) Fragmentation Buddy Weighted Buddy Buddy Weighted Buddy Internal 26% 12% 28% 14% External 1% 22% 1% 8% Total 27% 34% 29% 22%
Table 1. Simulation Results Comparing Fragmentation of the Buddy and Weighted Buddy Algorithms.
Table 1 gives the statistics for storage fragmentation for both the uniform and exponential block size distributions. For uniformly distributed block requests, the weighted buddy method achieves a significant savings in internal fragmentation but at a greater expense in external fragmentation. However, the increase in total fragmentation is only about 7 percent. For exponentially distributed block requests, though, the weighted buddy method is better than the buddy method by about 7 percent overall. This is a result of a large decrease in internal fragmentation which offsets the minor increase in external fragmentation.
Figure 4 shows a partial memory map of one large subblock which existed during overflow with uniformly distributed block size requests. Overflow occurred when a request for a block of size 211 arrived. However, there were still at least 15 of each of the block sizes, 29 and 210, available. These were not being recombined in the manner, (29, 210) --> 3*29, (29, 3*29) --> 211, because they were not buddies. So that we could probe possible remedies to this problem, the variations listed in the following section were tested on parts of the weighted buddy method, in an attempt to reduce external fragmentation. These variations were not tested for exponentially distributed block requests since external fragmentation is small here.
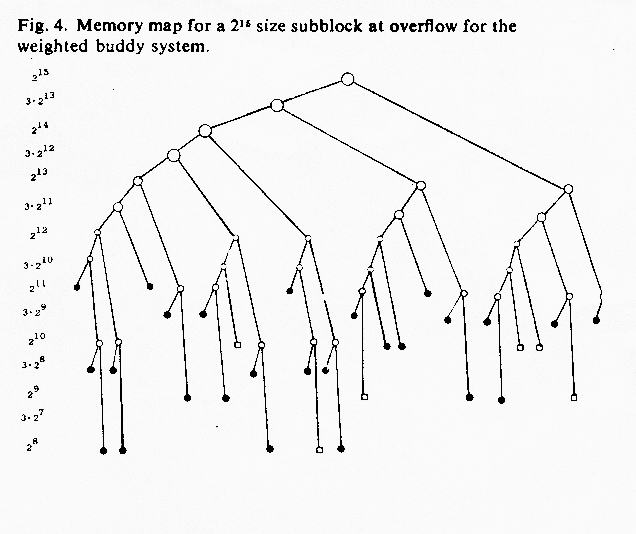
Figure 4. Memory map for a 215 size subblock at overflow for the weighted buddy system.
The first variation was on methods of continuing the splitting after finding a larger block to split. Instead of "continue splitting the smallest subblock greater than or equal to the desired size" as described in Section 2, we changed to the method discussed in VI below. The second variation was to change from a "queue" method (for inserting and removing equal sized blocks from the circular list attached to the ASL) to two other methods, as described in V2 and V3 below. The results of these variations were either worse or statistically insignificant.
The weighted buddy method presented in this paper is an alternative to the buddy method for dynamic storage allocation. The weighted buddy method allows the generation and use of nearly twice as many block sizes as the buddy method, and consequently it approximately halves internal fragmentation. This is achieved at an additional cost of only two bits per block and a possibly longer execution time. However, our simulation results show that external fragmentation may increase. Therefore, the trade-off between internal and external fragmentation, as well as the expected distribution of block sizes of the requesting processes, should be considered in a choice between these two methods of dynamic storage allocation. If the distribution of block sizes is skewed towards small block sizes, the weighted buddy method may be a better allocation algorithm.
This research also indicates that, although it would be possible to consider other methods of partitioning a memory block into subblocks, such new algorithms would probably result in a still greater external fragmentation and a higher execution time overhead than those used in the buddy system. It would be necessary to determine efficient means of defining the buddy of a block such as is achieved in both the buddy and weighted buddy methods by use of a partitioning which results in a suitable address form.
Acknowledgments. The authors are grateful to Thomas H. Bredt for his assistance with this research.
Received October 1973; revised May 1974
| Home | Comments? |