ACM Copyright Notice

Copyright © 1978 by the Association for Computing Machinery, Inc. Permission to make digital or hard copies of part or all of this work for personal or classroom use is granted without fee provided that copies are not made or distributed for profit or commercial advantage and that copies bear this notice and the full citation on the first page. Copyrights for components of this work owned by others than ACM must be honored. Abstracting with credit is permitted. To copy otherwise, to republish, to post on servers, or to redistribute to lists, requires prior specific permission and/or a fee. Request permissions from Publications Dept, ACM Inc., fax +1 (212) 869-0481, or permissions@acm.org.

ACM did not prepare this copy and does not guarantee that is it an accurate copy of the author's original work.

A new generation of computer terminals allow tab settings to be selected and set by the computer. This feature can be used to reduce the number of characters that are needed to represent a document for transmission and printing. In this note, an algorithm is given for selecting the optimal set of tab stops for minimizing the number of characters transmitted. An implementation of the algorithm has reduced the number of characters transmitted by from 7 to 30 percent, but requires a prepass through the document to compute a matrix used in determining the optimal set of tab stops. The use of fixed tab stops, as a heuristic alternative, can achieve about 80 percent of optimal with no prepass.

CR Categories: 3.9, 4.4

Keywords and Phrases: tabs, word processing, dynamic programming.

1. Introduction and Motivation

A new generation of computer terminals have appeared on the market in recent years which incorporate many advanced features. Of particular interest in this note are those terminals with variable tab stop settings. These terminals allow tab stops to be set, either manually or by computer, in a user-specified set of columns. If tabs have been set, a tab character (ASCII code 9) will move the terminal to the next tab stop (to the right).

The value of this feature lies in replacing long sequences of blanks by a single tab character, thus achieving a smaller, but equivalent, file. This savings can be important both as a means of text compression (fewer characters require less storage space) and as a means of achieving a higher effective transmission rate than may be allowed by available hardware. Specifically, several current printing terminals, based on the Diablo Hytype or Qume Sprint daisy wheel printing mechanisms, can print at 45, 55 or 60 characters per second. Connection to a computer system is commonly made by dial-up telephone lines, using modems limited to a maximum transmission rate of 300 baud (30 characters per second). This limitation on transmission speed leads to a desire to minimize the number of characters transmitted to print a given document, in order to increase the effective transmission rate and the throughput of the printer. Similar situations may exist in computer networks or time-sharing systems.

2. Reducing the Number of Transmitted Characters

The objective then is to process a text file prior to printing, and produce an equivalent file which takes advantage of the special features of the printer in order to minimize the number of characters to be transmitted across the communication line. Some obvious approaches include replacing all carriage return/line feed combinations by the unit separation code (ASCII code 31) which causes a carriage return/line feed with one character, setting a left margin to eliminate a constant set of blanks before each line (often used to move text away from the paper edge), and deleting trailing blanks. These changes are easily programmed.

A more interesting change results from replacing long sequences of blanks with tab characters. The strategy is to replace sequences of blanks by tabs, or sequences of tabs, perhaps followed by a shorter sequence of blanks. This will save k-1 characters whenever a sequence of k blanks is replaced by a tab. (Although there are both horizontal and vertical tabs, we limit our discussion here to horizontal tabs, which we refer to simply as tabs). Tab stops can be set in any column and a tab character will move the printer to the next preset tab stop. This provides a potential savings of many characters by replacing strings of blanks by tabs.

Caution must be exercised in the use of tabs, however. Any savings due to the use of tabs depends critically on the set of tab stops used. The appropriate set of tabs may vary from document to document. For listing a Fortran program, for example, a tab stop in column 7 would be most useful. Notice that a tab stop in column 6 could also be set, and would save the five blanks in the label field of a continuation card. However, continuation cards are relatively rare, and a tab stop in column 6 would double the number of tabs needed to get to column 7. Thus a tab in column 6 is probably not desirable. Tab stops in both columns 6 and 7 would be no better than a tab stop in column 6.

For a block structured language (such as Algol, Pascal, or PL/1) with an indented program text to reflect program structure, tabs should be set to follow the indentation.

The problem is to determine the optimal set of tab stops to minimize the number of characters needed to represent a document. The optimal set of tab stops will depend upon the length, position and frequency of blank character sequences.

3. The Algorithm

Define the upper triangular matrix M[i,j] to be the number of sequences of blanks which begin at or before column i and end in column j-1 (column j is the non-blank character terminating the sequence). Thus, a sequence of blanks in columns 11 through 13 will make a contribution to M[11,14], M[12,14] and M[13,14]. Notice that the sum over any row of the matrix is the total number of blanks in that column of the text.

If there is a tab stop in column t₁, with no other tab stops, then any sequence of blanks which starts before t₁ and ends at or after t₁ may have the sequence of blanks up to t₁ replaced by a tab to column t₁. Thus, a tab stop in column t₁, with no other tab stops, would result in saving,

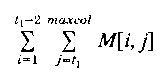
If we introduce a new tab stop in column t₂ (t₂ > t₁), we would increase the number of characters saved to,

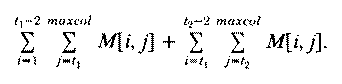
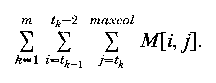
A visualization of this function is provided by Figure 1. Setting a tab stop in column t_i results in saving the sum of the entries in the box from rows t_i-1 to t_i-2 and from columns t_i to maxcol. (The sum stops at row t_i-2 instead of t_i-1 since the tab requires a character, so a string of k blanks is replaced by one tab, saving k-1, not k characters.)

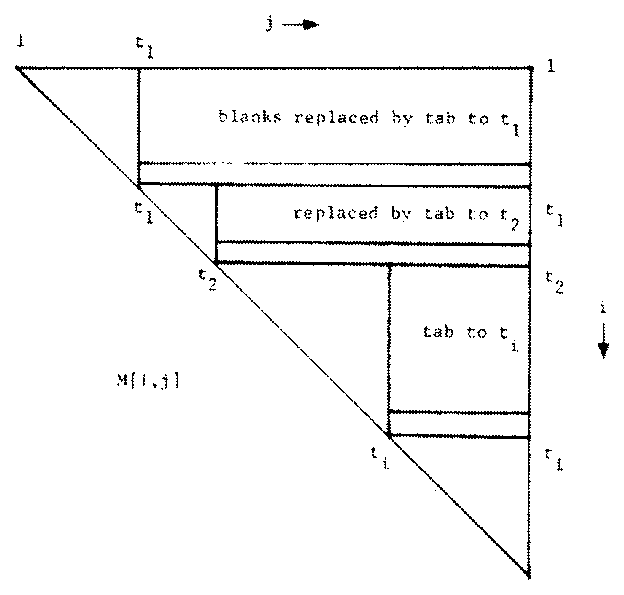
Figure 1. A representation of the savings which result from replacing sequences of blanks by tabs.

The important fact about this function is that a new tab stop can be added to the right of all other tab stops in the set of tab stops with the resulting savings depending only on the one tab stop to the immediate left of the new tab stop. This is clear from Figure 1 since the additional savings resulting from a tab stop in column t_i+1 is determined by the upper boundary of the rectangle above t_i+1. This upper boundary is t_i. This fact allows the optimal set of tab stops to be easily chosen using a dynamic programming approach.

The algorithm to determine the optimal set of tab stops from the matrix M determines, for each column k, the configuration of tab stops in the first k columns which result in the greatest savings, considering only configurations which include a tab stop in column k. The computation is done from left to right, so that the optimal configurations for columns 1 to k-1 are known when computing the optimal configuration with a tab stop in column k.

The optimal configuration with a tab stop in column k is determined by computing the savings which result from each of the columns 1, 2, ..., k-1 being the tab stop to the immediate left, and choosing from among these the column which gives the greatest savings. For each column k, we compute the savings resulting from a tab stop in column k, and the location of the tap stop to the immediate left of column k which gives the greatest savings for column k. The savings from a tab stop in column k is easily found using the savings for the previous columns, which have already been computed.

There is no cost resulting from a tab stop in column maxcol, so that some optimal setting of tab stops will include column maxcol. Thus, we find the best configuration with a tab stop in column maxcol; it contains a tab stop in maxcol, the best tab stop to the left of maxcol, the best tab stop to the left of this tab stop, and so on. By stepping back through the chain of best preceding tab stops, we determine the optimal set of tab stops.

4. Implementation and Evaluation

The algorithm was implemented by a program written in PASCAL and included as Appendix A. Care is taken so that summations over areas of the matrix are not recomputed. This is done by initially calculating and then incrementally updating the appropriate row sums of the matrix. This reduces the execution time for the algorithm to a quadratic function of the number of columns, O(maxcol²). Hence the processing time for a given file is essentially constant for tab stop selection. The production of the M matrix is linear in the length of the input.

In application, the algorithm can be quite successful. When executed on its own listing, the number of characters in the listing was reduced from 16,665 to 10,939, a reduction of 34 percent. This resulted in a consequent decrease in printing time when transmitted at our fixed transmission rate of 300 baud. Since the transmitted file was identical, when printed, to the unprocessed file, it could be said that the effective transmission rate was 457 baud, due to the compression. On a set of ten other Pascal programs, totaling 209,790 characters, an optimal set of tab stops reduced the number of characters by 63,524 or an average of 30 percent.

It should be pointed out that although even higher effective transfer rates can be achieved for extremely columnarized files, some files are not significantly compressed by the use of tabs, and only minimal savings may be achieved. For example, the algorithm was run on the text of this paper, and the original 11,895 characters were reduced by 755 characters to 11,140 characters, a savings of less than 7 per cent. On a larger sample of ten chapters of an assembly language programming text book, comprising some 772,905 characters, a savings of 58,597 characters (7.5 percent) was realized. Savings at this level are probably of minimal usefulness, considering the computational costs of the algorithm and the need for a prepass.

5. Alternatives

Although our algorithm will generate the optimal set of tab stops for replacing strings of blanks by tabs, this is not the only strategy for producing a minimal number of characters to represent a document. For example, consider a long string of blanks which ends just before the position of a tab stop. It would be possible to tab beyond the end of the blank sequence, to the tab stop, and then back-space back to the end of the blank sequence. In some cases this will result in fewer characters to be transmitted and hence would be an improvement over the strategy used here. However, the equations for an optimal set of tabs using spaces, tabs and backspaces would be more complex than the equations for tab stops using only spaces and tabs. One of the major drawbacks of the current algorithm may be the rather high cpu costs to compute the optimal set of tab stops.

An obvious alternative to computing optimal tab stops would be the use of fixed tab stops. The savings which result from fixed tab stops every n columns (column n+1, 2n+1, ...) were calculated, as a function of n, for both the set of ten programs and the ten text book chapters. The results are shown in Figures 2 and 3. As can be seen, although optimal tab stops can do significantly better than fixed tab stops, fixed tab stops can provide reasonable savings for minimal cost. This heuristic would appear to be approximately 80 percent of optimal.

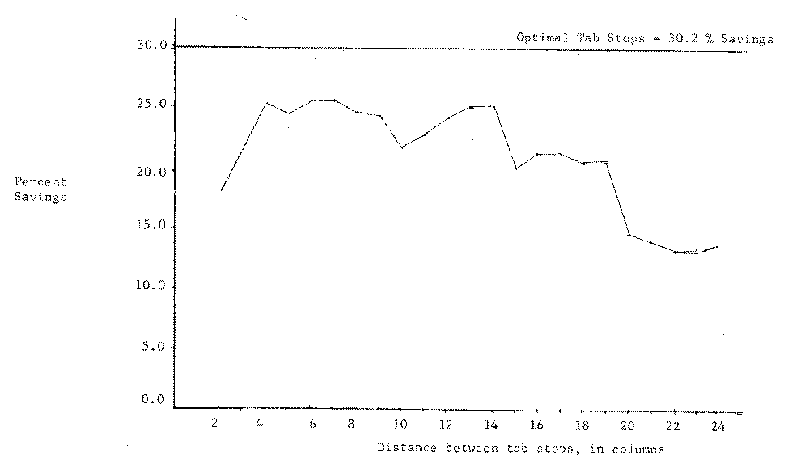
Figure 2. Savings resulting from the use of fixed tab stops, as a function of the tab stop distance, for a set of ten Pascal programs.

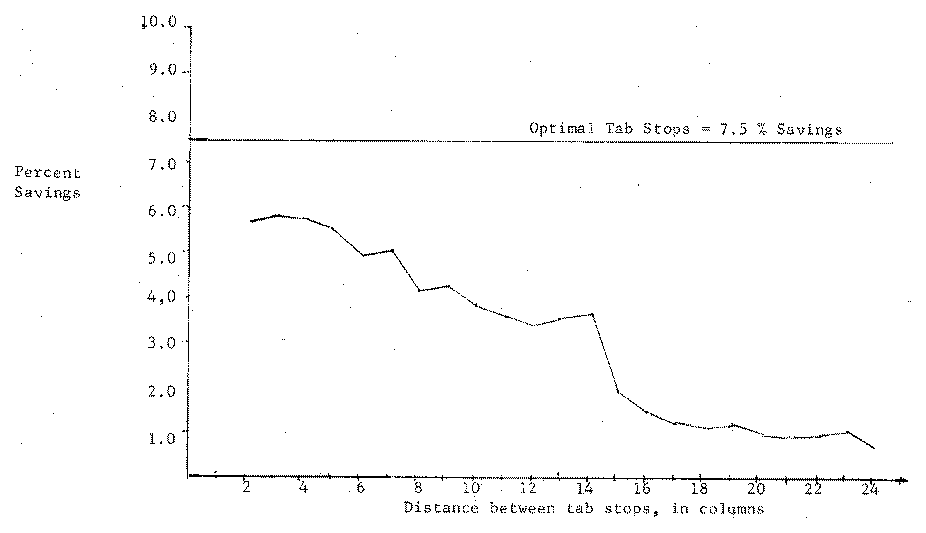
Figure 3. Savings resulting from the use of fixed tab stops, as a function of the tab stop distance, for a set of ten chapters of a textbook.

6. Summary

We have presented an algorithm for determining the optimal set of tab stops for representing a document in a minimal number of characters, by replacing sequences of blanks by tab characters. The algorithm can result in substantial savings in storage space, and transmission time, but at a cost of substantial computational overhead. Test runs show that selecting a fixed set of tab stops can produce savings which are 80 percent of optimal, and thus, in most instances, a fixed set of tab stops would be recommended.

Appendix. A Pascal procedure for calculating optimal tab settings

procedure definetabs;

   (*   This  routine  calculates  the optimal set  of  tabs
	and  defines  the array  tab.   tab[i] is the column
	to which a tab in column i will move.  The algorithm
	for  choosing  the tabs  involves  using  a  dynamic
	programming  approach  for choosing  the optimal set
	of tabs.                                          *)

var
	M:  array [1..maxcol,1..maxcol] of integer;
	save:  array[1..maxcol] of integer;
	previoustab:  array[1..maxcol] of 0..maxcol;
	rowsum:  array[1..maxcol] of integer;

	total:  integer;
	i, j, col:  0..maxcol;
	sum:  integer;

begin

	(* initialize for picking tabs *)

	save[1] := 0;	previoustab[1] := 0;
	save[2] := 0;	previoustab[2] := 0;

	sum := 0;
	for j := 3 to maxcol do sum := sum + M[1,j];
	rowsum[1] := sum;

	(* The rowsum array is used to avoid  recomputing  sums
	   in  M.   At  the  beginning of each iteration of the
	   following   loop,   romsum[1],    rowsum[2],    ...,
	   rowsum[col-2] are defined, with rowsum[k] = M[k,col]
	   + M[k,col+1] + ...  + M[k,maxcol].  For each  column
	   (col),  we calculate the gain (save) from a tab stop
	   in that column and the best previous  tab  stop  for
	   this column (previoustab).                        *)

	for col := 3 to maxcol
	 do begin
		total := 0;
		for i := 1 to col-2
		 do total := total + rowsum[i];
		save[col] := total;
		previoustab[col] := 0;

		for i := 2 to col-1
		 do begin
			total := total - rowsum[i-1];
			rowsum[i-1] := rowsum[i-1] - M[i-1,col];
			if total+save[i] > save[col]
			  then begin
				save[col] := total + save[i];
				previoustab[col] := i;
			       end;
		     end;


		sum := 0;
		for j:=col+1 to maxcol do sum:=sum + M[col-1,j];
		rowsum[col-1] := sum;
	end;

	(* create tab array *)

	j := maxcol;
	while j   0
	   do begin
		    i := previoustab[j];
		    for col := i to j-1
		     do tab[col] := j;
		    j := i;
	       end;

	tab[maxcol] := maxcol+1;

end;