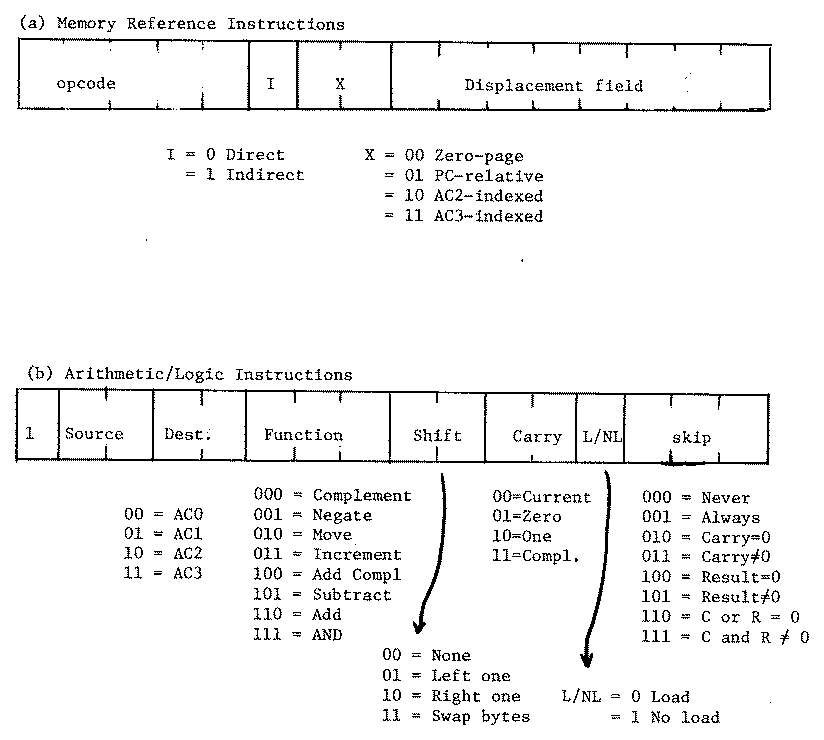
Figure 1. Instruction format for Nove 3/D. (a) Memory Reference and (b) Arithmetic/Logic Instructions.
| Home | Up | Questions? |
A compiler is being written to translate a Pascal-like language
into assembly code for the Data General Nova 3/D computer. A previous
note [1] has described the language and the basic structure of the
compiler. In this note, we describe the code generation problems
encountered and their solution.
The code generation problem is to determine appropriate sequences of assembly language instructions and data structures to properly implement the semantics of a higher-level language, in this case, of Pascal. Three general approaches are typically used for minicomputer compilers. The first is to generate all code (except I/O) in-line. This has the advantage of speed, but may require a lot of space if the translation is not straightforward. The opposite approach is to compile into a compact intermediate code which is then interpreted by a special system routine. This approach generally sacrifices speed for space, and is used mainly when the language semantics are quite different from the machine operations (such as with LISP, SNOBOL, or APL). A third approach, gaining in popularity, is a merger of these two approaches, where simple operations (like loading and assignments) are implemented in-line, while more complex instructions (like multiplication or procedure calls) are executed by system subroutines.
For the Pascal compiler, we have decided to generate all code in-line. This allows a program to be independent of system subroutines. The problems which need to be solved then involve data allocation and addressing, arithmetic operations, flow of control and procedure calls. After a brief review of the NOVA architecture, we discuss each of these points in turn.
The Nova cpu may have up to 32,768 16-bit words of memory. Integers are represented in two's complement, allowing a single precision integer range of -32,768 to +32,767. Characters are represented in ASCII, and may be packed, two to a word.
Four 16-bit registers (AC0, AC1, AC2, and AC3) are provided. All registers can be used for most operations, and so they can be considered as general-purpose accumulators. Two of the registers (AC2 and AC3) can be used as index or base registers. A one-bit carry register is also provided.

Figure 1. Instruction format for Nove 3/D. (a) Memory Reference and (b) Arithmetic/Logic Instructions.
There are three main classes of instructions: memory reference, arithmetic and logical, and I/O; the compiler only generates the first two kinds. Figure 1 shows the instruction format for these two instruction classes. For memory reference instructions, the operation specified by the opcode is performed between the register and the contents of the effective address. For arithmetic/logic instructions, the operation selected by the function field is performed between the source register and the destination register, with the result placed back in the destination register.
The effective address calculation for memory reference instructions is based upon one of four addressing modes, selected by the two-bit mode field, and the 8-bit displacement field. The four addressing modes are: (00) zero-page, (01) PC-relative, (10) AC2-indexed, and (11) AC3-indexed. In zero-page mode, the displacement field specifies one of the first 256 words of memory, addresses 0 to 255. PC-relative addressing adds the 8-bit displacement as a signed two's complement number, to the program counter, to form the effective address. This allows up to 128 locations before or 127 locations after the current instruction to be addressed. The two remaining modes allow register AC2 or AC3 to serve as a base register or index register which is added to the 8-bit, signed, two's complement displacement.
Addressing mode Effective Address Range --------------- ----------------------- zero-page 0, ..., 255 PC-relative PC-128, ..., PC+127 AC2-indexed AC2-128, ..., AC2+127 AC3-indexed AC3-128, ..., AC3+127.
The memory reference instructions are,
LDA (M) -> R.
STA (R) -> M.
ISZ (M)+1 -> M; if (M)=0 then skip next instruction.
DSZ (M)-1 -> M; if (M)=0 then skip next instruction.
JMP M -> PC.
JMS PC+1 -> R, M -> PC.
The arithmetic/logic instructions operate on a source register and a destination register, putting the result back into the destination register. Since no address is needed, the "address field" is used to specify the function to be performed. This is done by a series of small fields which select separate small actions. These small actions can be combined to form a larger composite instruction. Figure 2 illustrates the cpu organization for arithmetic/logic instructions. The fields of the arithmetic/logic instruction control: the source and destination registers to be used, the carry value used (current value, zero, one or complement), the function to be performed, how the result should be shifted (none, left, right, or swap bytes), and which conditions of the resulting carry and result will cause the next instruction to be skipped (zero, non-zero).
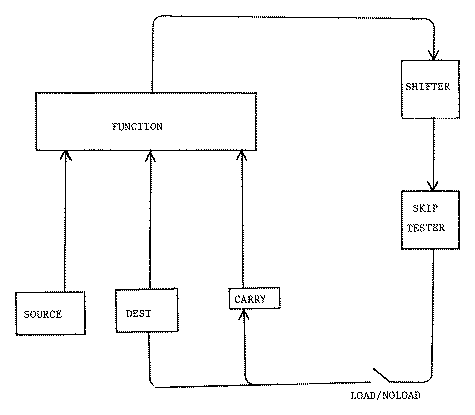
Figure 2. CPU organization of the Nova 3/D.
In summary, the Nova architecture is similar in many ways to the architecture of the PDP-8, but with some important advantages: word length (16 bits instead of 12), registers (4 instead of 1), addressing modes (4 instead of two (zero/current page)), and arithmetic functions. However, as we will see in the remainder of this note, despite these apparently modern architectural features, the Nova computer is very poorly designed with respect to compilation of a higher-level language.
The specific addressing modes of the Nova (zero-page, PC-relative, AC2-indexed, and AC3-indexed) raise serious problems in the addressing of data locations and instructions within a program. Instruction addressing should be solvable with PC-relative addressing, and is therefore left to Section 5, flow of control.
The block structured nature of Pascal, the desire for a self-compiling compiler, and the use of recursion in the compiler dictated a stack allocation scheme for local variables. Since total memory space for the stack will certainly exceed 256 words, zero-page addressing cannot be used, and so AC3 is dedicated as a stack pointer for the frame of local variables. The strategy is to allocate for each new procedure a frame on the stack which will hold all local variables for that procedure. AC3 will point to the bottom of the frame, and the stack pointer to the top. When the procedure is exitted, the stack pointer will be reset to AC3, and AC3 will be reset to point to the base of the previous frame.
This introduces one of the first problems with the Nova architecture. The displacement for AC3 addressing is a signed displacement ranging from -128 to +127. However, there is no legitimate reason to allow negative indexing into the stack; this would intrude into the stack frames of previous routines. If the compiler cannot use negative offsets, then we are restricted to no more than 128 variables per frame.
An alternative is to bias all offsets by -128, and bias register AC3 by +128. This puts register AC3 pointing to the "middle" of the current stack frame and allows the entire range of displacements to be used. However, the SAV and RET instructions, for procedure calls, explicitly reset AC3 to point to the frame base. Trying to maintain AC3 pointing to the middle of the frame would require resetting AC3 (at least two instructions) after every procedure call and return.
A limitation to no more than 128 variables is extremely restrictive: one array indexed by an ASCII character would exceed that capability. However, it is less likely that any one procedure would use more than 128 separate variable names. An entire array has only one variable name, and only arrays have more variables than names. Thus, arrays are allocated at the end of the stack frame, with a pointer to the base element stored in the addressable portion of the stack frame at the beginning. All array accesses are made indirectly through the one-word address, and only this one-word need be directly accessible. This reduces the number of words which must be addressable from all variables to all names. The limit of 128 names does not seem overly restrictive.
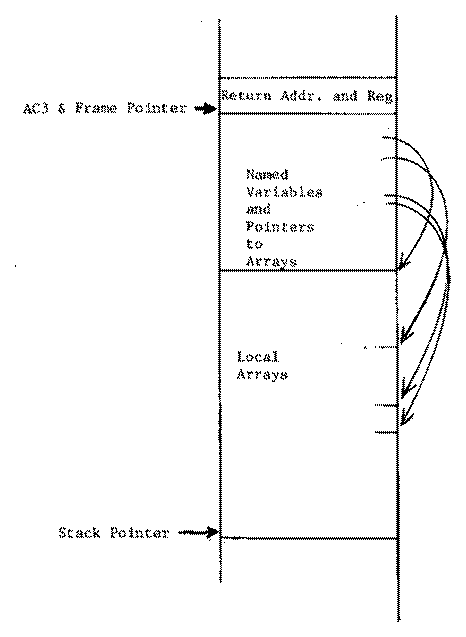
Figure 3. Frame structure showing array allocation and access method.
This frame structure is used for the local variables of each procedure, and the use of AC3 as a pointer to the base of the current stack frame allows local variables to be immediately accessible. Remember, however, that the block structure of Pascal allows a programmer to reference variables which are declared in outer procedures. A procedure at level i may reference variables at level 0, level 1, ..., level i-1. These variables will be on the stack in the stack frame for the appropriate procedure. To access one of these variables requires accessing the appropriate frame base pointer. To allow this, an array of frame pointers is kept in low core (zero-page). This array is indexed by level number and yields the most recent frame pointer for that level. Each procedure must store its frame pointer in the element for its level upon procedure entry, and restore the previous value upon procedure exit.
Statistics from the first Pascal compiler indicate that although a procedure at level i may reference any lower level, in fact, it seldom references variables other than at level i (local) and level 0 (global). Thus, the cost of accessing non-local variables is important only for global variables. Partly because of this, global variables are not put on the stack, but are allocated on zero page and accessed directly by zero-page mode addressing. As with local variables, arrays are allocated after non-array variables and accessed through a one-word pointer stored with non-array variables.
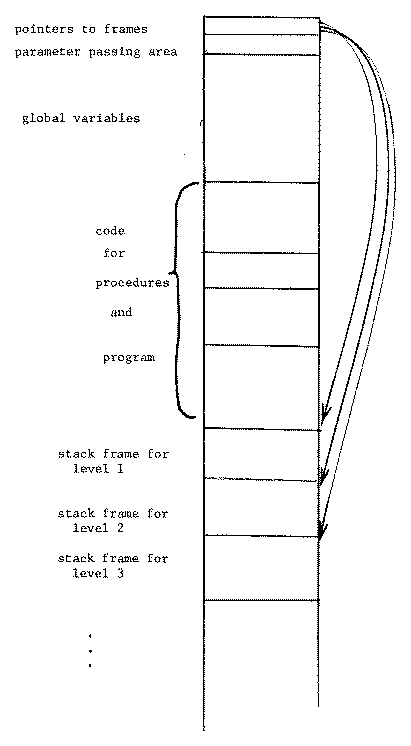
Figure 4. Overall representation of memory for a Pascal compiled program.
A last addressing problem is raised by the use of constants. Constants could be put on the stack, but this would require initializing them upon procedure entry. They could be allocated in the program, but only after the program since the use of a constant may occur undeclared at any time. However, for a long procedure, it may not be possible to directly address due to the limited size of the displacement field. Thus, what is needed is an immediate instruction. To avoid executing the constant requires a jump over it, the constant, and the load into a register, as,
JMP .+2 <constant> LDA r,.-1This three word accessing is required for all accesses to constants.
All code for arithmetic operations involves the use of the arithmetic/logic instructions and hence is strictly register to register. Although, in theory, there are four general registers available, there are in practice few register allocation problems. Register AC3 is permanently allocated to addressing local variables. Register AC2 must be used for all array accesses, accessing non-local variables and VAR parameters, and for certain arithmetic operations (multiply, divide, and compare). This leaves only registers AC0 and AC1, which are allocated as needed.
Instructions exist for addition and subtraction, so at first glance these two functions are easily implemented. However, on a small machine, overflow is a constant problem, and on this machine, no reasonable solution to the overflow problem exists. When adding two numbers, the only possible indicator of overflow is the carry bit. However, the carry is merely complemented when a carry out of the high order bit occurs.
Since the number representation is two's complement, overflow is signalled by a carry out of the sign (high-order bit) which differs from the carry in. Another form of the same statement is that the signs of the inputs are the same and differ from the sign of the output. Both of these conditions are easily tested in hardware; neither is easily tested in software. For the sake of expediency, the compiler does not currently check for overflow.
Multiplication and division are also clumsily implemented by the hardware. The architecture requires that, for multiplication, the two operands be in registers AC1 and AC2. The contents of AC1 is multiplied by AC2, added to AC0 and stored back in AC0 and AC1 as a double register product. The entire operation ignores the two's complement nature of the multiplication. For compiled code, this requires loading AC1 and AC2, clearing register AC0 and multiplying.
For division the opposite occurs: the double register (AC0, AC1) is divided by AC2 with the integer quotient put in AC1 and remainder put in AC0. Again the two's complement representation is ignored.
One important problem for compiler writers deals with the desired output from a comparison. Typically, the syntax of the language refers only to a boolean expression which may be used either in flow-of-control statements (IF-THEN-ELSE, WHILE-DO, REPEAT-UNTIL) or in assignment to a Boolean variable. In the former case, the desired output is a means to jump to a label, in the latter case, a zero (false) or non-zero (true) is desired for assignment. Complicated logical conditions (AND, OR and NOT operators) do not make things easier for jumps. Thus a common ploy is to always generate a zero or one for a test result. This can result in rather inefficient code for conditional flow-of-control code.
The comparison of two expressions to form a boolean expression is more common in many programs than arithmetic. Yet this is one of the more difficult code generation problems for the Nova architecture. There is no compare instruction, requiring that the compiler generate code to subtract the two values and test the result for zero, non-zero, positive or negative. This process is severely hampered by the inability to adequately detect overflow.
The cases of equality and non-equality tests are the easiest. If the result of the subtraction is zero, then the numbers were equal; if not, they were not. The code for an equality test requires three instructions; for non-equality, two.
For greater and greater-or-equal comparisons, five instructions are necessary. Because of the overflow problem, it is first necessary to set the carry bit to the exclusive-or of the sign bits of the operands. Then the subtract will produce a carry bit which defines the greater or lesser nature of the two operands.
Less than and less than or equal comparisons are translated into greater or equal and greater than compares by interchanging the operands.
The logical operations of AND and NOT can be relatively directly implemented. The OR operator can be implemented by negating the two operands, ANDing, and negating the result (4 instructions), or by ADDing the two results and skipping on the zero/nonzero status of the result (two instructions).
The compiled code to implement flow of control functions consists of the evaluation of boolean expressions (already considered in the last section) and the generation of appropriate jumps and conditional jumps. Since we are compiling into assembly code, the forward reference problem is not important, we simply generate labels and jumps to these symbolic labels.
An interesting point about all of the control structures of Pascal (IF-THEN-ELSE, WHILE-DO, and REPEAT-UNTIL) is that conditional jumps jump only on a false value of the controlling boolean expression.
The only problem here is the question of addressability. Not every location in memory is directly addressable, hence PC-relative addressing must be used for jumps. However, this allows references only to addresses within -127 or +128 locations of the current one. With no knowledge of the size of an IF-THEN-ELSE branch, or a WHILE or REPEAT loop, we must generate conservative code which assumes that the jump address may exceed the limit of PC-addressability. Thus all jumps are indirect jumps, using the next word as the jump address. This causes problems for conditional jumps which must use skips which jump over only one word. it is necessary in this case to jump conditionally on the opposite condition over the indirect jump, requiring four instructions.
<skip on false> JMP .+3 JMP @.+1 <address of label>
The result of this is that a simple IF I>2 for a local variable I will requires 12 instruction for the comparison and jumps.
Note that the problem of a limited jump range and needing a two-word jump for "long" distances is made worse by the one-pass nature of the compiler, since no knowledge is available about the length of forward jumps. However, even a two-pass compiler could not generate optimal code for this problem. Notice that on the first pass it is not possible to exactly determine the addresses of all labels. An address which follows a jump may vary depending upon the "long" or "short" nature of the jump, which is not yet known. Thus it is possible only to obtain upper and lower bounds on the addresses of labels. On the second pass, those labels whose upper bound still allows a short jump are obviously short, those whose lower bound requires a long jump are obviously long. But the remainder may be long or short depending upon the resolution of jumps which occur between the jump and its label. Thus additional passes are necessary to resolve the problem. There is no limit to the number of passes which may be needed, and this complexity is a direct result of the computer architecture.
Current programming methodology tends to favor the creation of many small procedures. Thus, the procedure call mechanism is very important for a higher-level language like Pascal. Efficient procedure calling requires adequate hardware support. Some help is provided by the JSR instruction which puts the return address in register AC3, the SAV instruction which stores all register on the stack and updates the hardware frame and stack pointers, and the RET instruction which resores all registers from the stack. However, the addressability problem again requires an indirect jump, because of the limited range of PC-relative addressing.
Parameter passing is a major problem. Parameters may be passed by value or by address (VAR). The general solution is to pass addresses to the procedure which then copies value parameters into local variables. The problem with this approach is the cost of generating an address on the Nova. The address of a local variable is a constant plus the frame pointer, requiring up to four instructions to load the constant and add.
The location of parameter addresses is also a concern. Placing them following the procedure call in the program code invokes forward references and non-reentrant code. Placing them on the stack requires removing them after the call (by a long sequence of POPs or a long loading of constant, stack pointer, and subtracting to reset the stack pointer). It was decided that a more efficient mechanism is to pass the parameter addresses in a special low-core (zero-page) area. This places a compiler limit on the maximum number of allowed parameters, but a limit of ten or sixteen should cause no great inconvenience.
The prologue of a procedure also requires the proper initialization of the pointers to local arrays, and the updating of the stack pointer.
The language under consideration is a limited subset of Pascal; limited to allow reasonable implementation on most small computers. However, the effort to generate code for the Nova computer reveals that the basic architecture of this computer is very unsuited for direct compiled code. The arithmetic/logic instructions ignore the signed nature of its integer operands leading to complex and lengthy code to detect overflow and to compare numbers. The limited addressability of the machine causes difficulties in the management of constants and arrays. Of the over 300 instruction mnemonics listed for the Nova computer, only 34 are useable for compilation.
The Nova computer appears to be a classic example of archaic machine-oriented computer design, totally unsuited for the application of modern computing techniques.
| Home | Comments? |