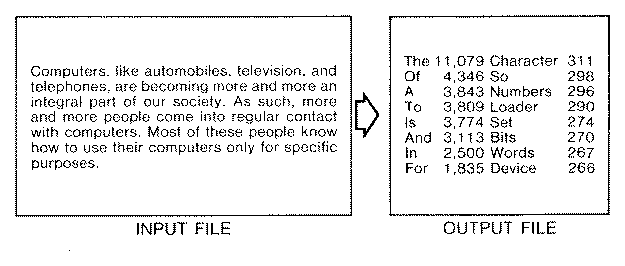
Figure 1. Constructing a word list. The words have been ordered by number of occurrences.
| Home | Up | Questions? |
Copyright © 1978 by the Association for Computing Machinery, Inc. Permission to make digital or hard copies of part or all of this work for personal or classroom use is granted without fee provided that copies are not made or distributed for profit or commercial advantage and that copies bear this notice and the full citation on the first page. Copyrights for components of this work owned by others than ACM must be honored. Abstracting with credit is permitted. To copy otherwise, to republish, to post on servers, or to redistribute to lists, requires prior specific permission and/or a fee. Request permissions from Publications Dept, ACM Inc., fax +1 (212) 869-0481, or permissions@acm.org.
ACM did not prepare this copy and
does not guarantee that is it an accurate
copy of the author's original work.
With the increase in word and text processing computer systems,
programs which check and correct spelling will become common. Several
of these programs exist already. We investigate the basic structure
of these programs and their approaches to solving the programming
problems which arise when such a program is created. This paper
provides the basic framework and background necessary to allow
a spelling checker or corrector to be written.
Computers can assist in the production of documents in many ways. Formatting and editing aid in producing a high quality document. Appropriate software can be devised to improve the appearance of output on typewriters and line printers. Use of sophisticated output devices, such as computer driven phototypesetters, xerographic printers, or electrostatic printers, can produce documents of outstanding quality.
Computers are being extensively used for document preparation. The systems used are typically a time-shared computer system with their file systems, text editors and text formatting programs. The author can enter the document directly on-line with the text editor, storing it in the computer's file system. The document has formatting commands indicating appropriate margins, spacing, paging, indenting, and so on. The text formatter interprets this to produce a file suitable for printing. The text file can be modified using a text editor which is generally an interactive program, while the formatter is more often a batch program.
This method of document preparation has created a market for word processing systems. This market will grow as more people apply computers to improve their document preparation.
Once this mode of document preparation is adopted, several new operations on text files become possible. Our interest here is in the possibility of analyzing documents for spelling errors. Several systems can analyze a text file for potential spelling errors, pointing out probable correct spellings. We expect spelling programs to be a standard part of all future text processing systems. Several companies, including IBM, have recently announced systems including spelling programs.
There are two types of spelling programs: spelling checkers and spelling correctors. The problem for a spelling checker is quite simple: Given an input file of text, identify those words which are incorrect. A spelling corrector both detects misspelled words and tries to find the most likely correct word. This problem has elements of pattern recognition and coding theory. A solution is possible only because of redundancy in the English language.
Each word can be considered a point in a multi-dimensional space of letter sequences. Not all letter sequences are words, and the spelling checker must classify each candidate word (called a token) as a correctly spelled word or not. We want to minimize errors, both of Type I (saying a correctly spelled word is incorrect) and errors of Type II (saying an incorrectly spelled word is correct). This involves a search of the word space to select the nearest neighbor(s) of the incorrectly spelled word. (This view of words in a multi-dimensional space can lead to peculiar representations of words such as in [Giangardella, et al 1967] in which each word is represented as a vector in a 2-dimensional space.)
Spelling errors can be introduced in many ways. The
following three are probably most important.
Different sources of errors suggest that some algorithms will be better for some errors.
Author ignorance. Such errors would lead to consistent misspellings, probably related to the differences between how a word sounds and is spelled.
Typographical errors on typing. These would be less consistent but perhaps more predictable, since they would be related to the position of keys on the keyboard, and probably result from errors in finger movements. Studies have shown that large data bases may have significant keyboarding errors [Bourne 1977].
Transmission and storage errors. These would be related to the specific encoding and transmission mechanisms. Early work in spelling correction was often aimed at the problem of optical character recognition (OCR) input [Bledsoe and Browning 1959; Harmon 1962; Vossler and Branston 1964; Carlson 1966; Rosenbaum and Hilliard 1975] and the recognition of Morse code [McElwain and Evans 1962].
The original motivation for research on spellers was to correct errors in data entry; much early work was directed at finding and correcting errors resulting from specific input devices in specific contexts. Davidson [1962] was concerned with finding the (potentially misspelled) names of passengers for a specific airline flight. Either (or both) name might be misspelled. Carlson [1966] was concerned with names and places in a genealogical data base. Freeman [1963] was working only with variable names and keywords in the CORC programming language while McElwain and Evans [1962] were concerned with improving the output of a system to recognize Morse code. Each of these projects considered the spelling problem as only one aspect of a larger problem, and not as a separate software tool on its own.
Many academic studies have been made on the general problem of string matching and correction algorithms [Damerau 1964; Alberga 1967; Riseman and Ehrich 1971; Wagner and Fisher 1974; Riseman and Hanson 1974; Lowrance and Wagner 1975; Wong and Chandra 1976], but not with the aim of producing a working spelling program for general text.
Recently several spelling checkers have been written for the sole purpose of checking text. Research extends back to 1957, but the first spelling checker written as an application program (rather than research) appears to have been SPELL for the DEC-10, written by Ralph Gorin at Stanford in 1971. This program, and its revisions, are widely distributed today.
The UNIX operating system provides two spelling checkers: TYPO and SPELL. These are different approaches. Another spelling checker has been written for IBM/360 and IBM/370 systems and is in use at the IBM Thomas J. Watson Research Center at Yorktown Heights. [Late addition: ispell ]
This paper reports on an investigation of these programs: how they work and their advantages and disadvantages. As a result, we determined how a spelling checker can be written using existing software technology. On the basis of this study, we then proceeded to write our own spelling checker/corrector using a top-down programming methodology [Peterson 1980].
The simplest assistance in checking spelling is an algorithm which lists all distinct tokens in the input. This requires a person to identify any misspellings. A program of this sort is a simple exercise.

Figure 1. Constructing a word list. The words have been ordered by number of occurrences.
Tokens which include numbers are often ignored by spelling checkers. This includes both tokens which are totally numbers ("1978", "10", and so on), and tokens which are part number and part letter ("3M", "IBM360", "R2D2", and so on). Whether these sorts of tokens should be considered by a speller might be best left as an option to the user.
Hyphens are generally considered delimiters; each part of the hyphenated token is considered a separate token. This follows from the normal use of a hyphen to construct compound words (such as "German-American", "great-grandmother", "four-footed", and so on). Hyphenation at the end of a line is best not allowed in the input to a spelling checker, since it should be well known that it is not possible, in general, to undo such hyphenation correctly.
Apostrophes are generally considered to be letters for the purpose of spelling correction. This is because of their use as an indicator of omitted letters (as in "don't" and "I'd"), and possessives ("King's" and "John's") An apostrophe at the beginning or end of a token might be considered a delimiter, since they are sometimes used as quote markers (as in: "the token 'ten' ..."), but plural possessives also have apostrophes at the ends of words ("kids'").
Another concern is for the case of letters in a token. Most frequently all letters will be in lower case, although the first letter is capitalized at the start of a sentence. Since "the" is normally considered the same word as "The", most spellers map all letters into one case (upper or lower) for analysis. A flag may be associated with the token to allow proper capitalization for spelling correctors, since we want the capitalization of corrected tokens to match the capitalization of the input token. Thus "amung" should be corrected to "among" while "Amung" is corrected to "Among".
The case problem is actually more complex because of the existence of words, particularly in computer literature, which are strictly upper case (such as "FORTRAN" and "IBM") and the widespread use of acronyms ("GCD" and "CPU") which are upper case. Should "fortran" or "ibm" be considered misspellings or separate words? What should be the cases of the letters used to correct an input token such as "aMunG"? These problems are minor but need thought in designing spelling correctors. Spelling checkers need only report that "aMunG" is not correctly spelled in any case; this allows all tokens to be mapped into a uniform case for checking.
A separate problem is a possible decision that tokens which consist solely of upper case characters should (optionally) not even be considered by a spelling corrector since they will most likely be proper names, variable names, or acronyms, none of which would typically be understood by a spelling program anyway.
Once these decisions are made, it is relatively straightforward
to create a list of all distinct tokens. The
basic algorithm is:
Initialize. Get the name of the input file and the output file, open them, and set all variables to their initial state.
Loop. While there are still tokens in the input file, get the next token, and enter it into an internal table of tokens.
To enter the token, first search to see if it is already in the table. If not, add it to the table.
Print. When all tokens have been read, print the table and stop.
The key to this program is obviously its internal table of tokens. We need to be able to search the table quickly and find a token (if it exists), or determine that it is not in the table. We also need to be able to add new tokens to the table, though we need not delete them. The speed of the program is most dependent on the search time. A hash table approach would seem the most reasonable for the table.
The table would be most useful if it were sorted. Sorting can be either alphabetically or by frequency. Attaching a frequency count to each table entry provides the number of uses of each token. This can speed the process by searching higher frequency items first (a self-modifying table structure); it also may give help in determining misspellings. Typographical errors are generally not repeated, and so tokens typed incorrectly will tend to have very low frequency. Any token with low frequency is thus suspect. Consistent misspellings (due to the author not knowing the correct spelling) are not as easily found by this technique.
This form of spelling program was used to check spelling for the text, Computer Organization and Assembly Language Programming, (Academic Press, 1978). Although it was quite tedious to check the resulting list of words (5,649 unique words out of 156,134 tokens), the result was a book with no (known) spelling errors.
An extension of this idea is the basis of the TYPO program on UNIX [Morris and Cherry 1975; McMahon, et al 1978]. This program resulted from research on the frequency of two letter pairs (digrams) and three letter triples (trigrams) in English text. If there are 28 letters (alphabetic, blank, and apostrophe) then there are 28 letters, 282 (= 784) digrams and 283 (= 21,952) trigrams. However, the frequency of these digrams and trigrams varies greatly, with many being extremely rare. In a large sample of text, only 550 digrams (70%) and 5000 trigrams (25%) actually occurred. If a token contains several very rare digrams or trigrams, it is potentially misspelled.
The use of digrams and trigrams to both detect probable spelling errors and indicate probable corrections has been one of the most popular techniques in the literature [Harmon 1962; McElwain and Evans 1962; Vossler and Branston 1964; Carlson 1966; Cornew 1968; Riseman and Ehrich 1971; Riseman and Hanson 1974; Morris and Cherry 1975; McMahon, et al 1978].
TYPO computes the actual frequency of digrams and trigrams in the input text and a list of the distinct tokens in the text. Then for each distinct token, an index of peculiarity is computed. The index for a token is the root-mean-square of the indices for each trigram of the token. The index for a trigram xyz given digram and trigram frequencies f(xy), f(yz) and f(xyz) is [log(f(xy)-1) + log(f(yz)-1)]/2 - log(f(xyz)-1). (The log of zero is defined as -10 for this computation.) This index is a statistical measure of the probability that the trigram xyz was produced by the same source that produced the rest of the text.
The index of peculiarity measures how unlikely the token is in the context of the rest of the text. The output of TYPO is a list of tokens, sorted by index of peculiarity. Experience indicates that misspelled tokens tend to have high indices of peculiarity, and hence appear towards the front of the list. Errors tend to be found since (a) misspelled words are found quickly at the beginning of the list (motivating the author to continue looking), and (b) the list is relatively short. In a document of ten thousand tokens only approximately 1500 distinct tokens occur. This number is further reduced in TYPO by comparing each token with a list of over 2500 common words. If the token occurs in this list, it is known to be correct and is not output thereby eliminating about half the distinct input tokens, producing a much shorter list.
The use of an external list (a dictionary) of correctly spelled
words is the next level of sophistication in spelling checkers.
The spelling checker algorithm using a dictionary is:
If the list of input tokens and the dictionary are sorted, then only one pass through the list and dictionary is needed to check all input tokens, providing a fast checker.
Initialize.
Build List. Construct a list of all distinct tokens in the input file.
Search. Look up each token of the list in the dictionary.
If the token is in the dictionary, it is correctly spelled.
If the token is not in the dictionary, it is not known to be correctly spelled, and is put on the output list.
Print. Print the list of tokens which were not found in the dictionary.
The major component of this algorithm is the dictionary. Several dictionaries exist in machine readable form. It may be most practical to use the output of the spelling checker to create the dictionary: i.e., a list of tokens which are not in the dictionary. Starting with a small dictionary, many correctly spelled words will be output by the checker. By deleting spelling errors and proper names from this list, we have a list of new words which can be added to the dictionary. A new dictionary can easily be created by merging the two.
The size of a reasonable dictionary can be estimated by the existence of books which list words, mainly for use by secretaries; e.g., [Leslie 1977]. These usually have from twenty to forty thousand words.
One must be careful not to produce too large a dictionary. A large dictionary may include rare, archaic or obsolete words. In technical writing, these words are most likely to be the result of a misspelling. Another problem with most large dictionaries is the tendency to include incorrectly spelled words. It is neither interesting nor pleasant to verify the correct spelling of 100,000 words.
A dictionary of 10,000 words should be quite reasonable for a small community of users. Since the average English word is about eight characters long, this requires about 100K bytes of storage. Controls will be needed on who may modify the dictionary.
The need for controls creates the post of system dictionary administrator. This person would be responsible for maintaining the shared system dictionary: the addition of new words and the selective deletion of those infrequently used.
One approach to limiting the size of the system dictionary is to create multiple dictionaries, one for each major topic area. This leads naturally to the concept of a common base dictionary with multiple local dictionaries of special words specific to a given topic. When a particular file is to be checked, a temporary master dictionary is created by augmenting the common base with selected local dictionaries. These local dictionaries can be created and maintained by the dictionary administrator or by individual users reflecting their own vocabularies.
The above algorithm for dictionary look-up is a batch algorithm. It is essentially the algorithm used for the UNIX and IBM spelling programs. There are some problems with this approach. First, a substantial real-time wait may be required while the program is running; this can be quite annoying to a user at an interactive console. Second, the output list of misspelled and unknown tokens lacks context. It may be difficult to find these tokens in the text using some text editors due to differences in case (for editors which pay attention to upper/lower case) and search difficulties (the file may be quite large, and/or the misspelled token may be a commonly occurring substring in correctly spelled words).
Problems such as those just discussed
can be easily corrected with an interactive
spelling checker. An interactive checker uses the following
basic algorithm.
This is the approach of the DEC-10 SPELL program and the approach which we used with our own spelling corrector.
Initialize. Possibly asking the user for mode settings and the names of local dictionaries.
Check. For each input token, search the dictionary.
If the token is not in the dictionary, ask the user what to do.
Several modes of operation may be available in an interactive checker. The interaction with the user may be verbose (novice users) or terse (experts familiar with the program). Local dictionaries of specialized terms may be temporarily added to the large shared system dictionary. A training mode (where all tokens are defined to be correctly spelled) may be useful for constructing local dictionaries.
The options available to the user
are determined by user needs. The following list indicates
some options:
Replace. The unknown token is taken to be misspelled and is to be replaced. The token is deleted and a correctly spelled word is requested from the user.
Replace and Remember. The unknown token is replaced by a user specified word, and all future uses of this token are also replaced by the new word.
Accept. The token is to be considered to be correct (in this context) and left alone.
Accept and Remember. The unknown token is correct and to be left alone. In addition, all future uses of this token are correct in this document; the user should not be asked about them again.
Edit. Enter an editing submode, allowing the file to be modified in its local context.
Use of a CRT as the terminal, lets the spelling checker display the context of an unknown token: at least the line containing the token should be displayed. On terminals with sufficient bandwidth and features, a larger context of several lines or an entire page can be displayed with the token emphasized by brightness, blinking, size or font.

Figure 2. An interactive spelling program as it might appear on a CRT terminal. Here, a page of text with a highlighted misspelled word, along with a list of corrective actions, are displayed.
The performance of an interactive spelling checker is important. The user is waiting for the checker and so the checker must be sufficiently fast to avoid frustration. Also, unlike batch checkers which need to look up each distinct token once (sorting them to optimize the search), an interactive checker must look up each occurrence in the order in which they are used. Thus, the interactive checker must do more work.
(It would be possible to batch small portions, up to say a page, of the input file. A list of all distinct tokens on a page would be created and the dictionary searched for each token. Each token which was not found would be presented to the user. This is repeated for each page in the input file. The main problems are with response time and in keeping track of the context of each usage of a token for display.)
The structure of the dictionary is thus of great importance. It must allow very fast searches. The "correct" structure must be determined for the configuration of the computer system. Such factors as memory size, file access methods, and the existence of virtual memory can be significant factors determining appropriate structures. If memory is large enough, the entire dictionary can be kept in memory, making operations easier and faster. If memory is virtual as opposed to physical, however, the dictionary structure should minimize page faults while searching. If memory is too small, a two-layer structure is needed, keeping the most frequently reference words in memory, while accessing the remainder with reads as necessary.
Algorithms and data structures for text processing may be tailored to the properties of the English language. Several studies have created large computer files of text which can be analyzed to determine the statistical properties of the language. The most commonly cited collection is the Brown Corpus [Kucera and Francis 1967] created at Brown University. The Brown Corpus contains 1,014,232 total tokens with 50,406 distinct words. The longest word is 44 characters, while 99% are 17 characters or less in length; the average word length is 8.1 characters. It is well known, however, that short words are used more frequently than long words. The ten most common words are "the", "of", "and", "to", "a", "in", "that", "is", "was", and "he". Because of this usage of shorter words, the average token length, when weighted by frequency of use, is only 4.7 characters, with 99% having 12 characters or less.
Knuth [1973] is a good source for different data structures and search algorithms. However, there is no "best" algorithm; each machine and each system makes different demands on the dictionary data structure. A few approaches are now outlined.
The DEC-10 SPELL program uses a hash chain table of 6760 entries. The hash function for a token is the first two letters (L1 and L2) and the length (WL) of the token (2, 3, ..., 10, 11 and over) as (L1*26 + L2) * 10 + min(WL-2,9). Each hash table entry is a pointer to a chain of words all of which have the same first two letters and the same length. (This program assumes all tokens of length 1 are correctly spelled.)
Another suggested structure for the dictionary is based on tries [Knuth 1973; Partridge and James 1974; Muth and Tharp 1977]. A large tree structure represents the dictionary. The root of the tree branches to 26 different nodes, one for each of the possible first letters of words in the dictionary. Each of these nodes would branch according to the possible second letters, given the known first letter associated with the node. These new nodes branch on possible third letters, and so on. A special bit would indicate the possible ends of words. This structure is particularly appropriate for small computer systems in which a token must be compared with a dictionary entry one character at a time. To search for a token of WL characters requires following the tree WL levels down and checking the end-of-word bit.
Alternative structures are generally based on the frequency of use of words. It is known that usage is extremely variable, and a small number of words are used most often. Hence, we want to structure our search strategy so that the most common words are searched first. One suggestion [Sheil 1978] is for a two-level search strategy.
In the two-level search strategy, the token would first be compared with entries in the small in-core table of most frequently used words. If the token is not in this table, a search would be made of the remaining words. This larger table might be stored on secondary disk or drum storage, or in a separate part of virtual memory, requiring longer access and search times. If this table is on secondary storage, access to a block can be accomplished by an in-core index.
From the Brown Corpus, we can determine the following
statistics for the percentage of
most common English words. The size of the table determines the
percentage of tokens found. As the table size is doubled,
a larger percentage are found.
Table Size Percent Tokens Found Gain ---------- -------------------- ---- 16 28.8 32 36.0 7.2 64 43.2 7.2 128 49.6 6.4 256 55.6 6.0
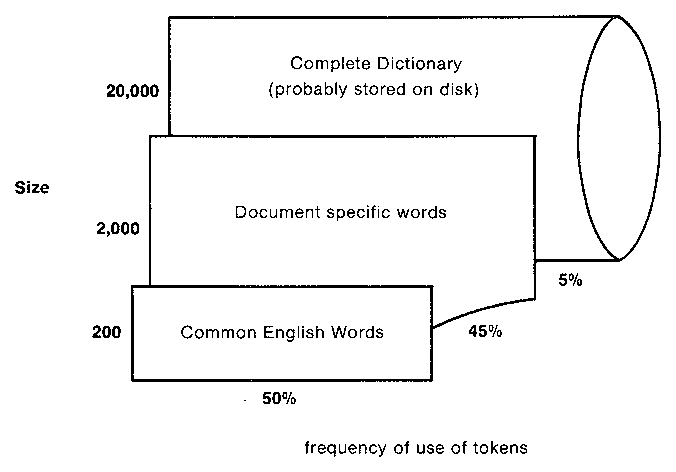
Figure 3. The possible size and use of three separate dictionaries.
Another improvement in search time can be made by noticing that
the total number of distinct tokens in a document tends to be
small to moderate (1500 for a 10,000 word document) and often
uses words of particular interest to the subject
area. This means that for each specific document, there exists a (small)
table of words which occur frequently in that document (but not
in normal English). Thus, it is wise to build another table of
words which have been used in this specific document. This three-table
structure would be searched by:
First, the small table of most common English words.
Next, the table of words which have already been used in this document.
Finally, the large list of the remaining words in the main dictionary. If a word is found at this level, add it to the table of words for this document.
Distinct data structures may be appropriate for these three
tables since they exhibit the following different properties.
Most common English words -- static, small (100-200).
Document specific words -- dynamic, small to moderate (1000-2000).
Secondary storage dictionary -- static, very large (10,000-100,000).
(You may recognize the latter two data structures as similar to a paging or segmentation scheme. Notice that even if the underlying computer system provides a virtual memory by such a memory management scheme, this data structure will provide improved locality and hence a lower fault rate.)
An interactive spelling checker can also be helpful in correction. In the simplest case, the checker remembers all tokens which the user indicates should be replaced, and the words with which they are to be replaced. After the first such replacement, future occurrences of the misspelled token can be automatically corrected, though this feature might be undesirable in some instances.
A similar approach is to include common misspellings in the dictionary with the correct spelling. Thus "greatfully" would be tagged as a misspelling of "gratefully" and "prehaps" as a misspelling of "perhaps". This approach has not been included in any current spellers: probably because of the lack of an obvious source of known misspellings and the low frequency of even common misspellings.
Most
misspellings can be generated from correct spellings by a few
simple rules. Damerau [1964] indicates that 80% of all
spelling errors are the result of:
1. transposition of two letters;
2. one letter extra;
3. one letter missing;
4. one letter wrong.
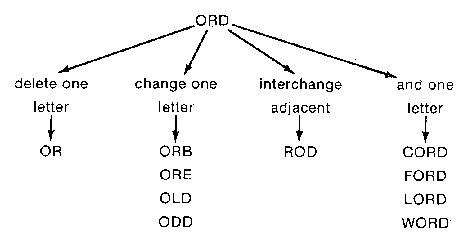
Figure 4. An illustration of an incorrectly spelled token and the correctly spelled tokens which result when certain simple rules are applied.
For each token which is not found in the dictionary, construct a list of all words which could produce this token by one of the above rules. These are candidate spellings.
If the list has exactly one candidate, guess that word, and ask the user if that word is the correct spelling.
If the list contains several words, state this. The user may then request the list and select one as the correct word, or indicate one of the normal options of replace, replace and remember, accept, accept and remember, or edit.
The candidate list is formed by multiple searches of the dictionary. Transpositions can be detected by transposing each pair of adjacent characters in the token, one at a time, and searching for the resulting token. If the resulting token is found, it is a candidate and is added to the list. For a token of WL characters, this requires WL-1 searches of the dictionary. Checking for one extra letter requires deleting each character one at a time, and searching for the resulting tokens. This requires an additional WL searches; most tokens are short (five characters on average) so this need not be expensive. However, no statistics are available on the average length of misspelled words.
The remaining two types of errors (one missing letter and one wrong letter) are difficult to detect. Two strategies are possible. The comparison operation can be defined to include a special match-any character. This means that a search for a missing letter could be achieved by inserting or appending the special match-any character and searching. The characteristics of this type of search are more complex than a simple bit-wise compare and will take more time. Considering the critical nature of performance, two separate searches may be needed: with and without the match-any character feature. A search with a match-any character feature cannot stop when the first word match is found, but must continue, since many words may match the token. This approach requires WL+1 searches for a missing letter error and WL searches for a wrong letter error.
A second approach is to substitute each potential character in each character position and search normally. If there are N potential characters (N approximately 27 depending on the classification of the apostrophe and similar characters), then a missing letter error requires N*WL+1 searches and a wrong letter requires N*WL searches.
A specific dictionary structure may allow improvements.
The DEC-10 SPELL program
separates the dictionary into 6760 chains by the first two
letters and length. For a token of length WL, candidate
spellings for one letter wrong and transposition errors are of
the same length, candidates for one letter extra errors are of
length WL-1, and one letter missing candidates are of length
WL+1. This considerably shortens the number of chains which
must be searched. The search strategy is best described by
quoting from the comments of the program itself.
"There are four kinds of errors that the program attempts to correct:
one wrong letter. one missing letter. one extra letter. two transposed letters.
For a wrong letter in the third or subsequent character, all words that are candidates must exist on the same chain that the suspect token hashes to. Hence, each entry on that chain is inspected to determine if the suspect differs from the entry by exactly one character. This is accomplished by an exclusive-or (XOR) between the suspect and the dictionary. Then a JFFO instruction selects the first nonzero byte in the XOR. This byte is zeroed and if the result is all zero then the dictionary word differs from the suspect in only one letter. All such words are listed at CANDBF, where they can be inspected later.
For a wrong letter in the first or second character, the program tries varying the second letter through all 26 possible values, searching for an exact match. Then all 26 possible values of the first letter are tried, after setting the second letter to its original value. This means that 52 more chains are searched for possible matches.
To correct transposed letters, all combinations of transposed letters are tried. There are only WL-1 such combinations, so it is fairly cheap to do that.
To correct one extra letter, WL copies of the token are made, each with some letter removed. Each of these is looked up in the dictionary. This takes WL searches.
To correct one missing letter, WL+1 copies of the token are made, each time inserting a null character in a new position in the suspect. The null character is never part of any word, so the suspect token augmented by an embedded null can be thought of as a word with one wrong letter (the null). Then the algorithm for matching one wrong letter is used. If the first character is omitted, all 26 possible first characters are tried. Also, 26 more tokens are formed by varying the second character in case that had been omitted."
Spelling correction is certainly not cheap. But it is not prohibitively expensive nor is it normally needed, only those tokens not found in the dictionary.
Other correction algorithms have been suggested. One theoretically pleasing suggestion [Alberga 1967] is to determine the lengths of common substrings in a token and a dictionary word. This can be used to determine an index of matching. The index of matching can be considered to be the probability that the token resulted from a misspelling of the dictionary word. The word with the highest probability can be selected as the most likely correct spelling. This seems to be a very expensive algorithm.
Similar algorithms have been investigated by Wagner and Fischer [1974] and Lowrance and Wagner [1975].
Additional information can often be used to increase correction accuracy or speed. One important source of additional information is the source of possible errors. For example, errors introduced by OCR input devices are only the substitution of one letter for another; characters are never inserted or deleted by the OCR reader. In addition, it is possible to create a confusion matrix giving the probability pi,j of reading a character i when the correct character is j. This confusion matrix can be used to indicate which characters should be considered when an input letter is to be corrected. In a more general system, digram and trigram frequencies could be used to limit the number of alternative spellings which must be considered.
The layout of the standard typewriter keyboard may also be of use in correcting errors introduced in keyboarding text.
Another technique attacks the problem of words which the original author spelled incorrectly. The misspellings in this case are often based on word sound. It has been suggested that tokens should be converted to standard phonetic spelling, which would be used to find similarly sounding words in the dictionary. This would help correct such apparent double errors as using "f" for "ph" or "k" for "qu".
On the other hand, correction based upon the four rules used by the DEC-10 SPELL program is quite successful and relatively cheap, leaving the more difficult corrections to the user.
For performance reasons, it is desirable to keep the dictionary in memory. Thus serious thought has gone into means of reducing the size of the dictionary. In the Brown Corpus of 50,406 words, half were used only once or twice. A dictionary of 8000 words would represent 90% of the words; 16,000 words would yield 95%.
A major reduction may be possible however by considering common affixes. (An affix is either a suffix or a prefix.) Most plural nouns and verbs result from adding an "-s" to the end of the singular form. Other common suffixes include "-ly", "-ing", "-est", "-er", "-ed", "-ion" and so on. By removing these suffixes and storing only the root word, the dictionary can be significantly reduced. Similar approaches are possible for prefixes.
Two approaches are possible. In the simplest case, each token is examined for a list of common affixes. These are removed if found. Hence any token ending in "-s", has the "-s" removed. (The order of search can assure that larger suffixes, like "-ness" are removed first.) Then the dictionary is searched. If found, the token is judged correct. A major problem with this approach is that it does not catch misspelled tokens which are the result of correct affixes incorrectly applied to correct words, such as "implyed" or "fixs". This can allow misspelled tokens to escape detection.
A solution to this problem is to flag each word in the dictionary with its legal affixes. Then the dictionary is first searched for the token. If the token is not found, it is examined for possible affixes. These are removed and the dictionary searched for the root. If the root is found, its flags are examined to see that the particular affix is legal for this root.
The rules associated with affix removal can be complex.
As an example, the following flags, and their interpretation
are used in the DEC-10 SPELL program. These rules show how
to add a suffix to a root word.
Let a and b be "variables" that can stand for
any letter. Upper case letters are constants. "..." stands for
any string of zero or more letters.
"G" flag:
...E --> ...ING
...a --> ...aING, if a is not E.
"J" flag:
...E --> ...INGS
...a --> ...aINGS, if a is not E.
"O" flag:
...E --> ...ED
...bY --> ...bIED, if b is not A, E, I, O, or U
...ba --> ...baED, otherwise.
"S" flag:
...bY --> ...bIES, if b is not A, E, I, O, or U
...a --> ...aES, if a is S, X, Z, or H
...a --> ...aS, otherwise.
Suffix removal requires the correct reversal of the above rules, showing how to produce a root and suffix from an input token. Similar rules are defined for prefix removal.
The interaction of affix removal and spelling correction is not well understood, nor is iterated affix removal (removing several affixes).
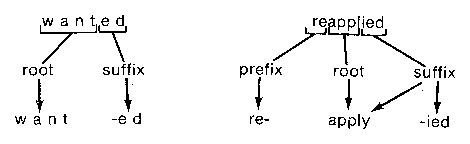
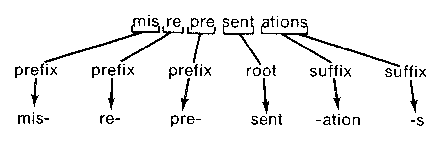
Figure 5. Prefix and suffix analysis iin a spelling corrector showing three different levels of difficulty.
Of the three spelling checkers, each uses a different approach to affix analysis. The IBM speller uses no affix analysis, preferring a larger but simpler dictionary. The UNIX speller removes a few common suffixes and prefixes with no check for the legality of these affixes on the resulting root. Some of the DEC-10 SPELL programs maintain the flags listed above.
Based upon the research on spelling programs recounted above, we implemented a program to check and correct spelling errors [Peterson 1980]. Our intent was twofold: (1) to produce a machine independent spelling program design, and (2) to test modern programming principles in the construction of a non-trivial program.
A spelling program is an excellent example for a programming project, especially for students. The concept of a program which detects (and possibly corrects) spelling errors in a text file excites students with its apparent intelligence. Yet in its simplest implementation, it is little more than a table look-up program. At the same time, advanced students can extend the project to almost arbitrary complexity.
Our spelling program is an interactive spelling corrector. A three-level dictionary of common English words (256 of them), a hash table of document words, and a disk-based dictionary is used. Local dictionaries are supported. The program was developed completely top-down in a Pascal-like pseudo-language.
The design consists of two parts. Starting with the main program, a text portion discusses the possible alternative designs and the decisions which lead us to our choice. This choice is then written in a code portion. The code portion uses procedure calls to represent those parts of the design yet to be completed. This approach is then repeated with the undefined procedures, alternating between a text discussion of the design and an eventual code representation of our design choice.
The result of this approach to design is a document which details not only what the program is, but also why the program has developed as it has. The design document serves to both describe and explain.
To implement the speller, a text editor was used to delete the text portion of the design document, leaving only the code portion. The text editor was then used to effect a massive inversion of the code. Note that a top-down design produces first the main program and then its subprocedures. This is the inverse order required by, for example, Pascal. Thus, it is necessary to completely reorder the procedures as produced by the top-down design.
In addition, the use of abstract data types resulted in associating data type and variable declarations with the few procedures and functions which actually use the data items. The declarations in a Pascal program must be at the beginning of the program, preceding all procedure declarations. This required additional movement of code. Finally, some limitations of the Pascal language (e.g. inability to use a set value in a case statement) were overcome by local recoding.
The result of this relatively mechanical editting of the design document was an executable Pascal program. There were no major errors; the errors were either syntactic (e.g. missing semicolons or index variable declarations) or due to failing to properly initialize some local variables.
There are still some problems with our spelling program, particularly in terms of performance. The program is somewhat sluggish. We are investigating the cause of this sluggish behavior, but feel it is probably the result of one or more of the following three factors:
The existing spelling checkers clearly demonstrate the feasibility of spelling checkers and correctors for English, and by implication, for similar languages. Suffix and prefix analysis for Romance languages might be easier and more necessary. The applicability of this work to German, Russian or Oriental languages is unknown.
The existence of a spelling checker and corrector suggests that
the next step is to build more knowledge into the checking
programs. The following checkers and
correctors are possible next steps.
Each checker would have an associated corrector which would attempt to correct the problem. These programs would greatly aid the preparation of documents, although they would be more difficult to construct.
Consistency. In some cases, several correct spellings exist for a given word, such as "grey" and "gray". In addition to assuring that all tokens in a file are correctly spelled, we should assure that a consistent spelling is used. In addition we should check that appropriate case is used on proper names such as IBM, Algol, Jim and so on.
Syntax. Given that we can identify words in a sentence, the next step is to classify each word according to its word class (noun, verb, adjective, article, and so on). Given this identification, the structure of each sentence can be checked to assure that each sentence is properly constructed and syntactically correct.
Grammar. Once syntax can be checked, we must check grammar. This includes spelling and syntax, but also proper usage of the words and punctuation.
Semantics. Finally, a program which examines a document for correct meaning would be useful. This program would check that the ideas in the document are properly developed and presented, that conclusions are correctly based on the facts presented (or known), that the document is complete and consistent and that the document contributes new information or insights into significant problems.
We have begun efforts to construct a syntax checker. The on-line dictionary is being expanded to include parts of speech for each word, and various table-driven parsing methods are being researched. There is a considerable question of how much syntax checking can be done without semantic information, particularly for such problems as number agreement and missing articles.
Discussions with William B. Ackerman, Robert Amsler, Michael H. Conner and Leigh R. Power have helped in the writing of this paper.
| Home | Comments? |