Figure 1. Number of Undetected Typing Errors
| Home | Up | Questions? |
Copyright © 1978 by the Association for Computing Machinery, Inc. Permission to make digital or hard copies of part or all of this work for personal or classroom use is granted without fee provided that copies are not made or distributed for profit or commercial advantage and that copies bear this notice and the full citation on the first page. Copyrights for components of this work owned by others than ACM must be honored. Abstracting with credit is permitted. To copy otherwise, to republish, to post on servers, or to redistribute to lists, requires prior specific permission and/or a fee. Request permissions from Publications Dept, ACM Inc., fax +1 (212) 869-0481, or permissions@acm.org.
ACM did not prepare this copy and
does not guarantee that is it an accurate
copy of the author's original work.
Spelling programs detect misspelled or mistyped words by checking each word against an approved word list. Any word not on the word list is assumed in error. Using a large word list avoids having correct words mistakenly thought to be errors. However, as the size of the word list grows, the probability of an undetected typing error also grows. The probability of an undetected typing error, weighted by the frequency, of the intended word varies from 2% to 16%. Thus, to minimize the chance that an incorrectly typed word is not found, the word list should be as small as possible. Balancing these opposing tendencies suggests that small, topic-specific word lists are most appropriate.
Computer programs to detect, and correct spelling and typographic errors are now fairly well understood and becoming quite common [Peterson 1980a]. The interesting problems now deal mainly with the details of the design: the data structures and user interface, and not with the basic algorithms. Work is already proceeding on the construction of more advanced techniques for detecting syntactic and semantic errors [Heidorn 1982; Cherry 1980].
Despite the obvious value of spelling checkers, there can be problems. Perhaps the most important problems are mistakes made by the spelling checker. As with all pattern recognition algorithms, mistakes can be of two kinds: (1) failure to accept a correctly spelled word, and (2) failure to reject an incorrectly spelled word. How bad are these problems?
Let us assume that the spelling checker is based upon a look-up algorithm: the spelling checker maintains a word list of correctly spelled words. To check a word, the speller simply searches this list. If the word is found, it is (assumedly) correctly spelled and hence accepted; if it is not found, it is (assumedly) incorrectly spelled, and hence rejected.
Clearly, with this algorithm, the speller will fail to accept correctly spelled words only if they are not on its list of approved words. To reduce the probability of this mistake, we can simply add more words to the approved word list, increasing its size. Ignoring the problems of storage and search time for large word lists, this approach may increase the probability of the second kind of mistake: failure to reject an incorrectly spelled word.
How can an incorrectly spelled word be mistakenly recognized as correct by a spelling checker? Assume that the author/user meant to use the word x, but mistyped the word as y. (For example, house may be mistyped as horse). This error will be undetected only if y is a correctly spelled word. It is admittedly not the desired word, but it is still a word on the approved word list. This kind of error can be detected only by more complex algorithms using syntactic or semantic information.
Simple look-up is not the only algorithm used by spelling checkers. Many spellers strip prefixes and suffixes from a word before looking up the resulting root. This allows 'swims' to be accepted by simply storing the root 'swim'. It may also allow 'swimed' to be accepted. Similarly Nix [1980] mentions an algorithm which uses multiple hash functions to save space, but at the cost of potentially accepting some incorrectly spelled words. Hence, the number of errors made by our assumed look-up algorithm is a lower bound for other algorithms.
The probability of misspelling or mistyping a word as another word, should increase as the size of the word list increases. As the size of the word list increases, more obscure and unusual words will be added to the list. These words will no longer be detected as errors but will be thought correct by the spelling checker.
This note reports on research to determine the probability that a word can be mistyped as another word, as a function of the size of the word list.
First, we must redefine the problem. In our previous research into spelling checkers [Peterson 1980b], we were unable to come up with any good information about how people misspell, so we have concentrated instead on how words are mistyped. The classical definition of typing errors by Damerau [1964] indicates that 80% of typing errors are caused by,
Our own studies have show similar results. We found 360 errors in a computer copy of Webster's Seventh Collegiate Dictionary [Peterson 1983] which had escaped detection since the file was keyboarded 15 years ago (including ten errors in the original printed version). We also found 155 errors made by college students when they retyped the word division list of the U.S. Government Printing Office [GPO 1968]. These errors were distributed as,
| GPO | W7 | |
| Transposition | 4 (2.6%) | 47 (13.1%) |
| One Extra | 29 (18.7%) | 73 (20.3%) |
| One Missing | 49 (31.6%) | 124 (34.4%) |
| One Wrong | 62 (40.0%) | 97 (26.9%) |
| Total | 144 (92.9%) | 341 (94.7%) |
The next most common errors were 2 extra letters, 2 missing letters, or 2 letters transposed around a third (such as prodecure instead of procedure).
Notice that although these results are similar, they are not sufficiently accurate or stable to provide good estimates of the probabilities of different kinds of errors or of key-level errors. There is almost certainly an error distribution for each key, due in large part to keyboard layout. Intuitively, a 't' is more likely to be mistyped as an 'r', than as a 'q', while a 'q' is more likely to be mistyped as an 'a' than an 'r'. We have assumed simply that these 4 types of errors are all equally likely.
Over the last few years, we have collected many word lists from different sources, including word lists from,
In all, we have some 16 word lists. These were merged to produce one master list of 369,546 words in a file of 3,799,425 bytes (an average of 9.3 characters plus a separator byte per word).
A program was written to read the master list of words and generate each of the possible "mistyped" versions of the word, according to the four main typing errors. Only one occurrence of one error per mistyping was considered. Each mistyped word was then checked to see if it was some other word. This program was executed, taking 5 days on a dedicated VAX 11/780 -- some 158,583.0 seconds of cpu time (about 44 hours).
The result of this program was a file of 15,609,965 bytes with 988,192 entries. Each entry consisted of two words and a code describing how one could be mistyped to be the other. Of the 369,546 unique words in our master list, 153,664 of them cannot be mistyped as some other word; 215,882 can be mistyped as some other word. In the extreme, for example, the word sat can be mistyped into 54 other words.
Of the 988,192 possible words that can be mistyped as another word,
| 616,210 | were due to one wrong letter. |
| 180,559 | were due to one extra letter. |
| 180,559 | were due to one missing letter. |
| 10,864 | were due to transposing two letters. |
(The numbers for one extra and one missing are the same since if word x can be mistyped as a word y by adding one extra letter, then y can be mistyped as x by deleting that extra letter. Similarly, the number of errors for wrong letters and transpositions should be even, as they are.)
How many typing errors are possible? For a word with n letters, each pair of adjacent letters can be transposed for n-1 possible errors. Similarly, the other typing errors could cause the following numbers of typing errors, assuming an alphabet of 28 characters (the 26 letters plus the hyphen and the apostrophe).
| one wrong | 27n |
| one extra | 28(n+1) |
| one missing | n |
| transposition | n-1 |
Thus 57n+27 typing errors are possible for a word of length n. This allows, for our master list of 369,546 words, 205,480,845 possible mistyped words. Since only 988,192 of these are words, the probability of mistyping a word as another word is 988,192/205,480,845 or about 0.5%, half a percent, for our full list.
Of course, no one uses our entire word list in a spelling checker; we need to repeat this study for smaller word lists. There are, however, 2369,546 sublists for a word list of 369,546 words. It would be impossible (and pretty useless) to do this for every such sublist. We assumed instead that a word list of length m would be the m most common words. Then any word on a list of size m would also be on each list of size m' > m. This allows us to determine the words in a word list as its size varies, if we know the frequency of the words.
There have been at least 3 major word frequency studies:
While these provided some frequency information, they were not broad enough to provide complete information. Only 22,439 words were on all three studies. To produce complete frequency information, we averaged the frequencies of the 3 major studies. Words which were in none of the studies were assigned a frequency corresponding to the number of times that they occurred in our set of word lists. This produced a frequency for each word ranging from 1 to 323,302,702. Summing these frequencies and dividing by the sum gives probabilities (ranging from 0.052 to 0.00000000016).
Sorting by frequency allows us to assign ranks to the words. The most frequent word is the, with of, and, to, a, in, is, that, it, and he completing the top ten. Some words have the same frequency (to the accuracy available from the existing studies). These words are all assigned the same rank. Thus the 27,943 words which occurred in only one word list were all assigned the same rank: 369,546.
Now assume that a word x of rank p can be mistyped as a word y of rank q. If p < q (that is, x is more frequent than y) then the mistake will be detected for all lists with only words of rank less than q. If the word list expands to q or more words, the mistake will go undetected. In general the mistake will be undetected if the length of the word list is greater than or equal to max(p,q).
For example, the word house is rank 139; horse is rank 577. Thus, if house is mistyped as horse, it will be undetected if the length of the word list is greater than or equal to 577. If horse is mistyped as house, it will also be an undetected error for a word list of more than 577 words. (In fact this error would be undetected for word lists from 139 to 577 words also, but in this case horse would not be considered a valid word; it is not on the word list. We have not considered the problem of mistyping a non-word as a word.)
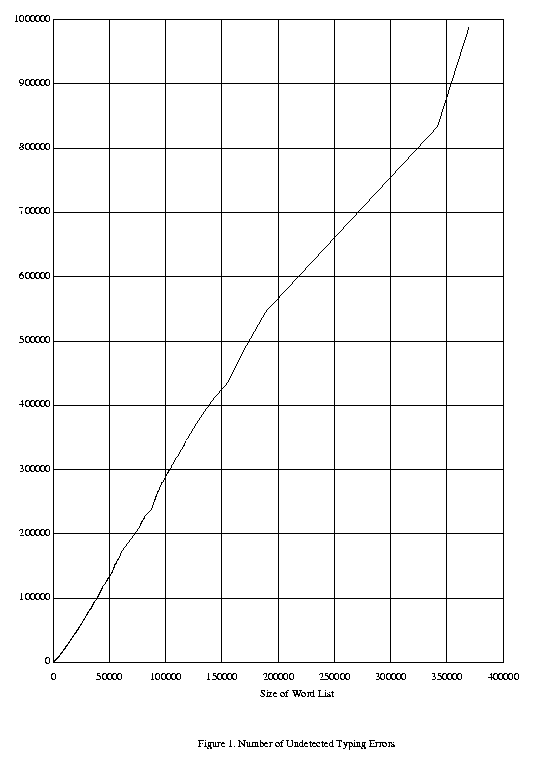
Figure 1 shows the number of undetected errors as the size of the word list varies, from 1 to 369,546 words. We see that the number of undetected errors appears to increase roughly linearly with the size of the word list. Clearly, however, the number of errors which are undetected will always increase as the size of the word list increases; undetected errors remain undetected as more words are added to the word list.
Figure 1. Number of Undetected Typing Errors
Perhaps we should look, not at the total number of undetected errors, but only the fraction of all errors which are undetected. As the word list grows, the probability would increase that a given mistyping would go undetected, but of course with more words on the word list, there are more possible mistypings also. Figure 2 shows the fraction of undetected typing errors as the word list varies. For a word list of size m, this is the number of undetected typing errors for m (from Figure 1) divided by the sum, over all m words in the list, of the number of possible typing errors (57n+27 for each word of length n). Although the fraction of undetected errors does increase as the word list grows to 50,000 or 60,000 words, it then levels off and is fairly stable, over the long run, at about 0.5 per cent.
Figure 2. Fraction of Possible Errors which are Undetected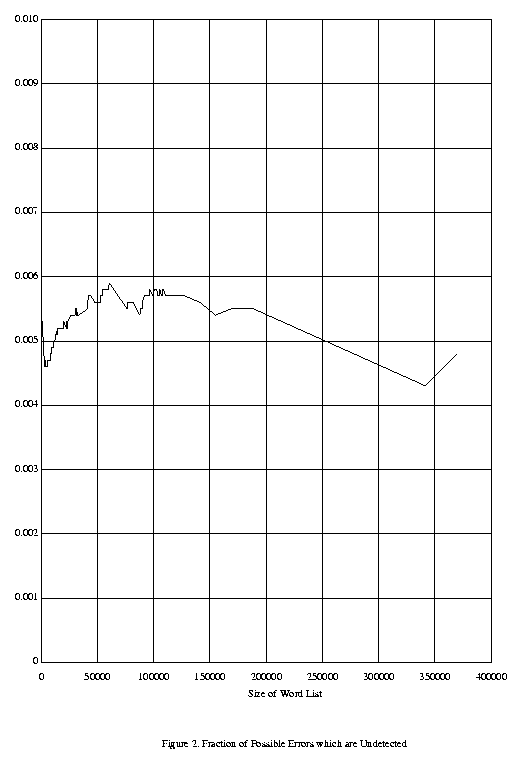
It would appear, then, that only one word out of every 200 mistyped words would accidentally become another word, escaping detection by a spelling checker.
However, this result ignores two important observations.
First, frequent words tend to be shorter than less frequent words. And second, short words, if mistyped, are more likely to be undetected than longer words, since proportionally more short words are on a word list. Of the 784 (28*28) possible 2-letter words, 431 (55%) are valid (in the complete 369,546 word list). On the other hand, only 21,611 words of 10 characters (out of a potential 296,196,766,695,424) are valid.
Our final figure reinforces the conclusion that most undetected typing errors come from the short frequent words which are in every word list. Figure 3 shows the probability of an undetected error, weighted by the frequency of the intended word. This measures the probability of an undetected typing error in running text. Since small words are both more frequent and more likely to produce undetected typing errors, the probability of undetected errors increases rapidly for the first 100,000 words and then grows much more slowly.
Figure 3. Fraction of Possible Undetected Errors Weighted by Frequency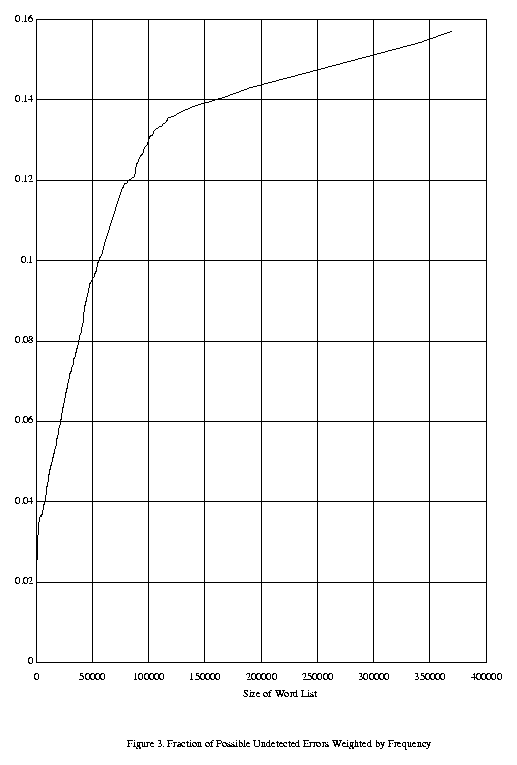
In actual usage, the probability of an undetected typing error varies directly with the size of the word list, ranging from 2% to almost 16% of all typing errors.
We want to remind you that these numbers are only rough indicators of the actual problem. While we used the best information available to us, the following questions are not well answered:
In addition, we would expect all of these quantities to vary with the author/typist.
Despite these unanswered questions and their effect on the actual probability of an undetected spelling error, it would seem reasonable to conclude that a significant number of spelling and typing errors may be undetectable by a spelling program.
There is a real danger that longer word lists will result in a substantial number of undetected typing errors. Almost 1 typing error out of 6 may be undetected. Accordingly, word lists used in spelling programs should be kept small. A large word list is not necessarily a better word list. In particular, word lists used for spelling should be tailored for the particular author and topic for which it is to be used. Word lists used for checking computer science papers should generally not include medical, legal, and geographic words, for example.
We can also see a need for more intelligent checking programs, such as syntax and semantics checkers. A simple spelling checker cannot detect a word which is mistyped as another word. More complex approaches (using part of speech information for example) may be able to detect such errors, however.
Finally, although programs can catch many spelling and typing problems, human proofreading is still necessary to detect and correct many errors.
This work was supported, in part, by the Department of Computer Sciences of the University of Texas at Austin, and the Computer Science Department of Carnegie-Mellon University.
| Home | Comments? |