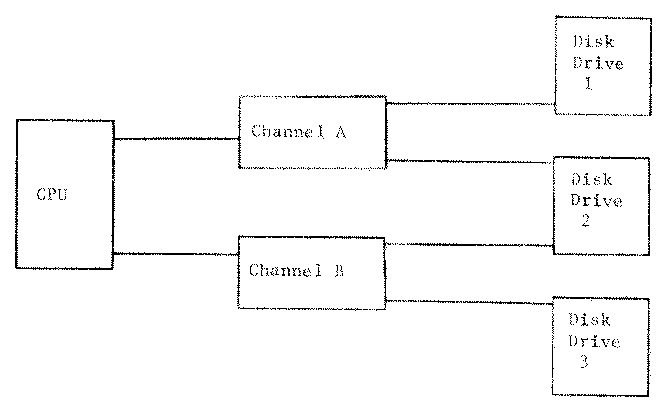
Figure 1 (a). Block Diagram of Shared Disk System.
| Home | Up | Questions? |
Several extensions to the basic Petri net model have been proposed. Some of these "extensions" (such as self-loops and multiple arcs) do not actually increase the power of the basic model, while other extensions (such as inhibitor arcs or priorities) do increase the class of systems which can be modelled. Recently several researchers have considered extending the model to allow colored or typed tokens [1,2,3,7]. In this note, we consider this extended Petri net model.
We refer the reader to [5] for an introduction to the Petri net model. Briefly, a Petri net is a four-tuple (P,T,I,O) where P is a finite set of places, T is a finite set of transitions, and I and O map T into bags of places. I(tj) defines the inputs of a transition tj; O(tj) defines the outputs of tj. A marking consists of a distribution of tokens to the places. A transition can fire if each of its inputs has a token (multiple tokens for places which are multiple inputs). The transition fires by removing the enabling tokens from its inputs and adding tokens to all of its output places (multiple tokens for multiple outputs).
When using a Petri net to model a system, tokens often represent objects or resources in the modelled system. As such, these resources may have attributes which are not easily represented by a simple Petri net token. For example, in Figure 1, we show a Petri net which models part of an operating system dealing with a disk system. One place represents the two channels (A and B) while another represents the three disk drives (1, 2 and 3). Although both channels are the same equipment model, and the three disk drives are similarly identical, the connections between them require that disk drive 1 must use channel A, while drive 3 must use channel B; drive 2 can use either channel A or B.

Figure 1 (a). Block Diagram of Shared Disk System.
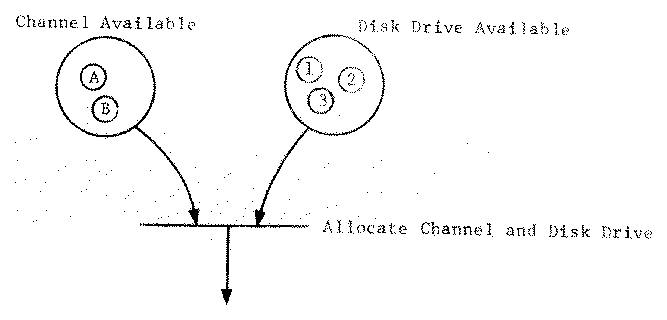
Figure 1 (b). Petri net representation of resources.
To model these systems with a standard Petri net may be difficult, and so we consider extending the model by allowing colored tokens. We define a set of colors, C. A marking now specifies, for each place, the bag of colored tokens at that place. (The use of a bag allows several tokens of the same color to reside in a place.)
The major question now is how to define the firing of a transition: how are the colors of the input tokens used to define the colors of the output tokens? Let qj be the number of input tokens and rj be the number of output tokens for a transition tj. We suggest that the most general firing rule defines for each transition tj a function fj of qj input tokens which produces an rj-tuple of output tokens. This can be represented by a table such as Figure 2.
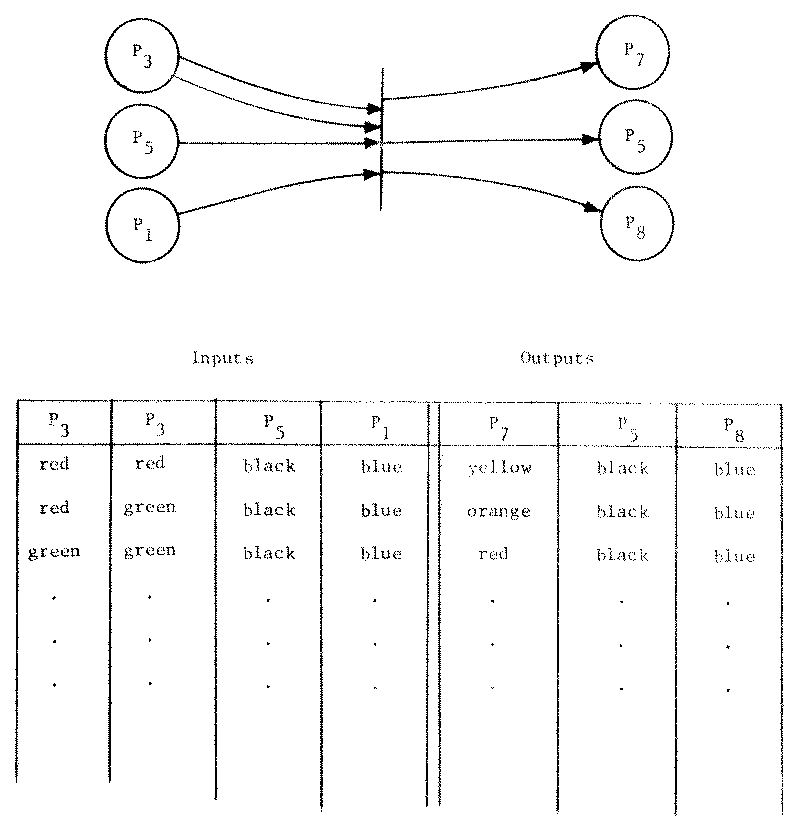
Figure 2. An example of the firing rule definition for a colored Petri net.
This extended Petri net model can easily model many systems which are naturally defined in terms of typed quantities or distinct individuals. Figure 3 is a model of a simple disk scheduling algorithm for the configuration defined in Figure 1.
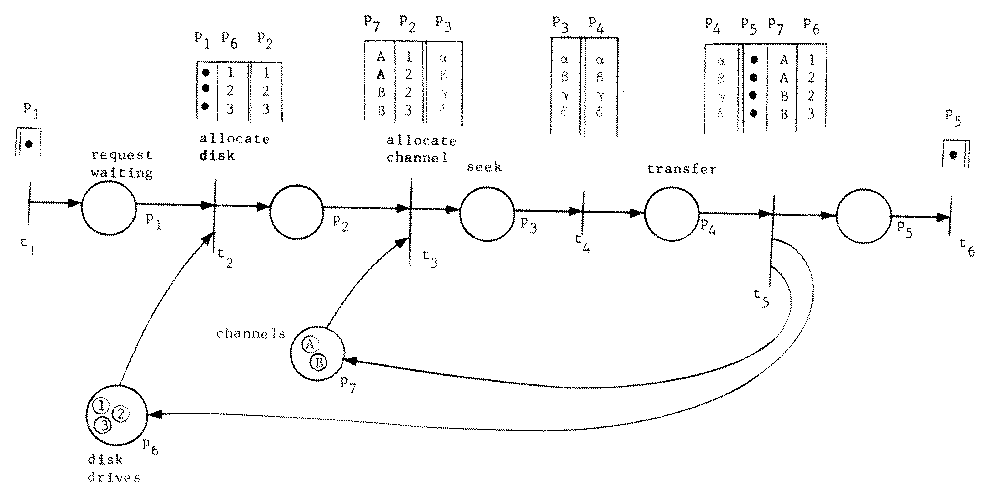
Figure 3. A simple disk scheduling algorithm modeled by a Petri net with colored tokens.
The question is whether this is a significant extension to the Petri net model. We consider two cases: a finite number of colors and an infinite number of colors.
If there are only a finite number, k, of distinct colors, we can convert a net with colored tokens (with the extended firing rule defined above) into an equivalent net with tokens of only one color (with the normal firing rule). Each place in the colored net is mapped into a set of places and each transition is mapped into a set of transitions in the new net. Hence, there is a homomorphic mapping from the new net, its state space and transition sequences into the old net, its state space and transition sequences, and an inverse homomorphic mapping in the other direction.
The new net is created by duplicating the colored net once for each color. Thus, for a place pi, we define a set of k places pi,1, pi,2, ..., pi,k. We then redefine transitions to interpret a token in pi,c to be a token of color c in place pi. Specifically, we define for each transition t in the colored net a new transition t' in the equivalent uncolored net. If the row of the table defines the inputs of t to be a token of color c1 from place p1, color c2 from p2, ..., and color cq from pq, then the inputs of t' are an (uncolored) token from each of p1,c1, p2,c2, ..., and pq,cq. Similarly for outputs of color cq+1 to place pq+1, color cq+2 to pq+2, ..., color cq+r to pq+r, then we define outputs to pq+1,cq+1, pq+2,cq+2, ..., and pq+r,cq+r.
Figure 4 is the uncolored Petri net equivalent to the colored net of Figure 3.
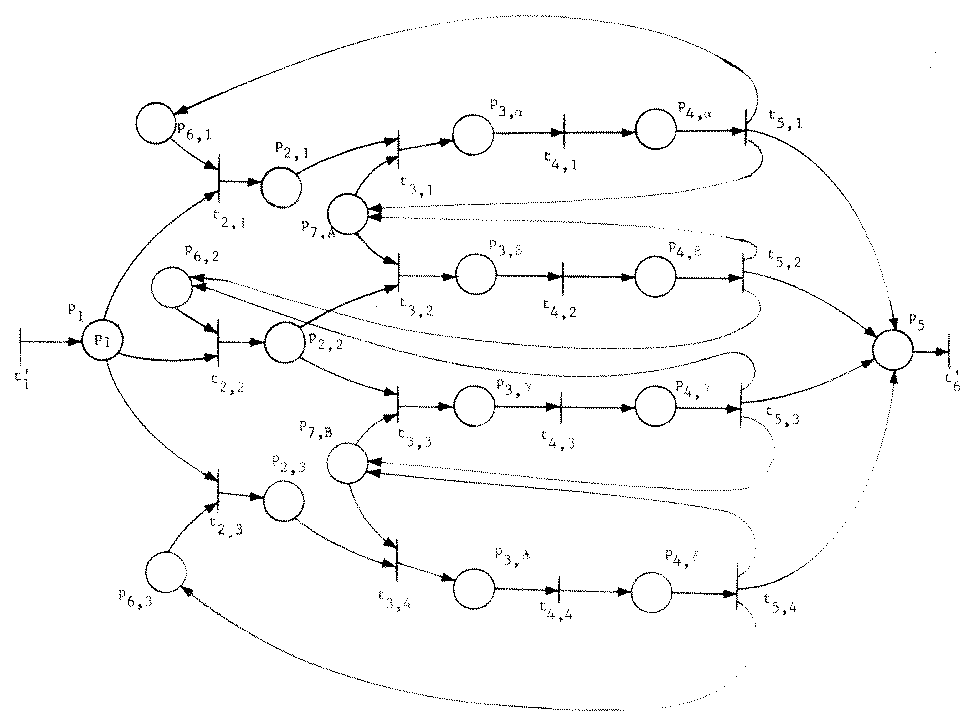
Figure 4. An (uncolored) Petri net which is equivalent to the colored Petri net of Figure 3.
This construction may produce large numbers of disconnected places which can then be discarded, but in general a colored net with k colors, n places and m transitions will produce an equivalent uncolored net with n.k places and up to m.kq+r transitions, where q is the maximum number of input places and r is the maximum number of output places for any transition.
This construction has also been considered in [3] and [4].
In this second case, when the number of colors is allowed to be infinite, it is fairly easy to define a net which uses the colors to represent the positive integers. (Let color ci represent the integer i, i > 0). Now we can use places to simulate registers by representing a value n in a register by a token of color cn in the place. With our ability to define the action of a transition separately for each color, we can construct transitions to add one to a place, to subtract one from a place, or to test for zero using the color encoding of the integers. These three functions on as few as three registers (places) have been shown to be sufficient for encoding Turing machines. Hence most interesting questions become undecidable. Thus, allowing an infinite number of colors extends the modelling power of the basic Petri net model.
If the transformation given above (for the case of a finite number of colors) is applied to a net with an infinite number of colors, an infinite Petri net is produced. Petri's thesis [6] showed that infinite nets can model Turing machines.
The use of colored tokens in a Petri net model can allow a much more concise model of a system. As long as the number of colors is finite, the model is equivalent to a (much larger) Petri net without colors. However, allowing an infinite number of colors results in an extended model equivalent to a Turing machine, for which most general questions are undecidable.
| Home | Comments? |