| Home | Up | Questions? |
In Chapter 3 we demonstrated that Petri nets can be used to model a wide variety of systems: computer hardware and software, chemical, social, and so on. However, this large set of examples only shows that Petri nets can model some systems; there may be systems which cannot be properly modeled as Petri nets. That is, there may be limits on the modeling power of Petri nets.
In addition, in Chapter 5 we have shown that not all analysis questions are decidable for Petri nets. The inclusion and equivalence problems for Petri net reachability sets and for Petri net languages are undecidable, but these problems may be very important for producing optimal Petri nets. Even those analysis questions which are decidable are very difficult, meaning that they require large amounts of computation.
In this chapter, we investigate the suggestions which have been made to overcome these two limitations on Petri nets: limitations on Petri net modeling power and limitations on Petri net decision power. We look first at some of the extensions to the Petri net model which have been suggested. Extending the Petri net model should increase the modeling power of Petri nets but may also decrease the decision power. The effects of any extension on the decision power of the extended model must be carefully considered.
Having then seen that extending the Petri net model may tend to reduce decision power, we also consider how decision power can be increased by restricting the Petri net model. Various subclasses of the Petri net model have been suggested. These models are produced by restrictions on the structure of the Petri net. We must examine the effect of these restrictions on both modeling power and decision power.
This investigation shows how modeling and decision power can
be traded, one for the other, and also indicates the limits
of both for the Petri net model.
7.1. Limitations of Modeling with Petri Nets
Several researchers who have used Petri nets to model systems have found them too simple and limited to easily model real systems. Thus, there has been a marked tendency to extend the model to make it easier to use. These extensions have been of several types.
Patil [1970a] suggested extension of Petri nets to include constraints. A constraint is a set of places. The firing rule is modified to allow a transition to fire if and only if the resulting marking does not have all of the places which are in a constraint simultaneously marked. For example, if { p1, p4 } is a constraint set, then either p1 or p4 must be empty at all times; if p1 is marked, then a token cannot be put in p4 until all tokens in p1 are removed and vice versa.
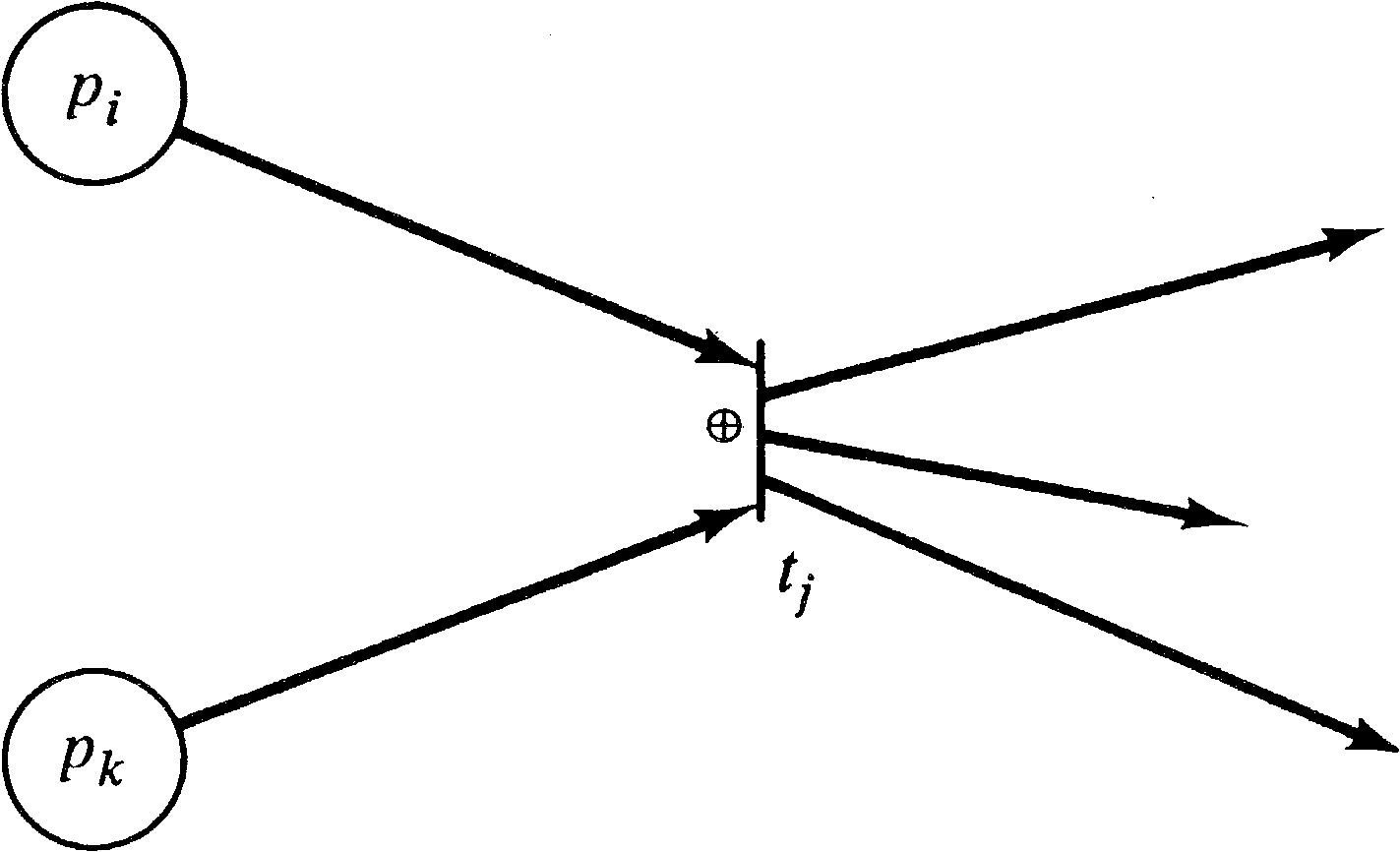
Noe, in his model of the CDC 6400 operating system [Noe
1971], introduced a different extension: the
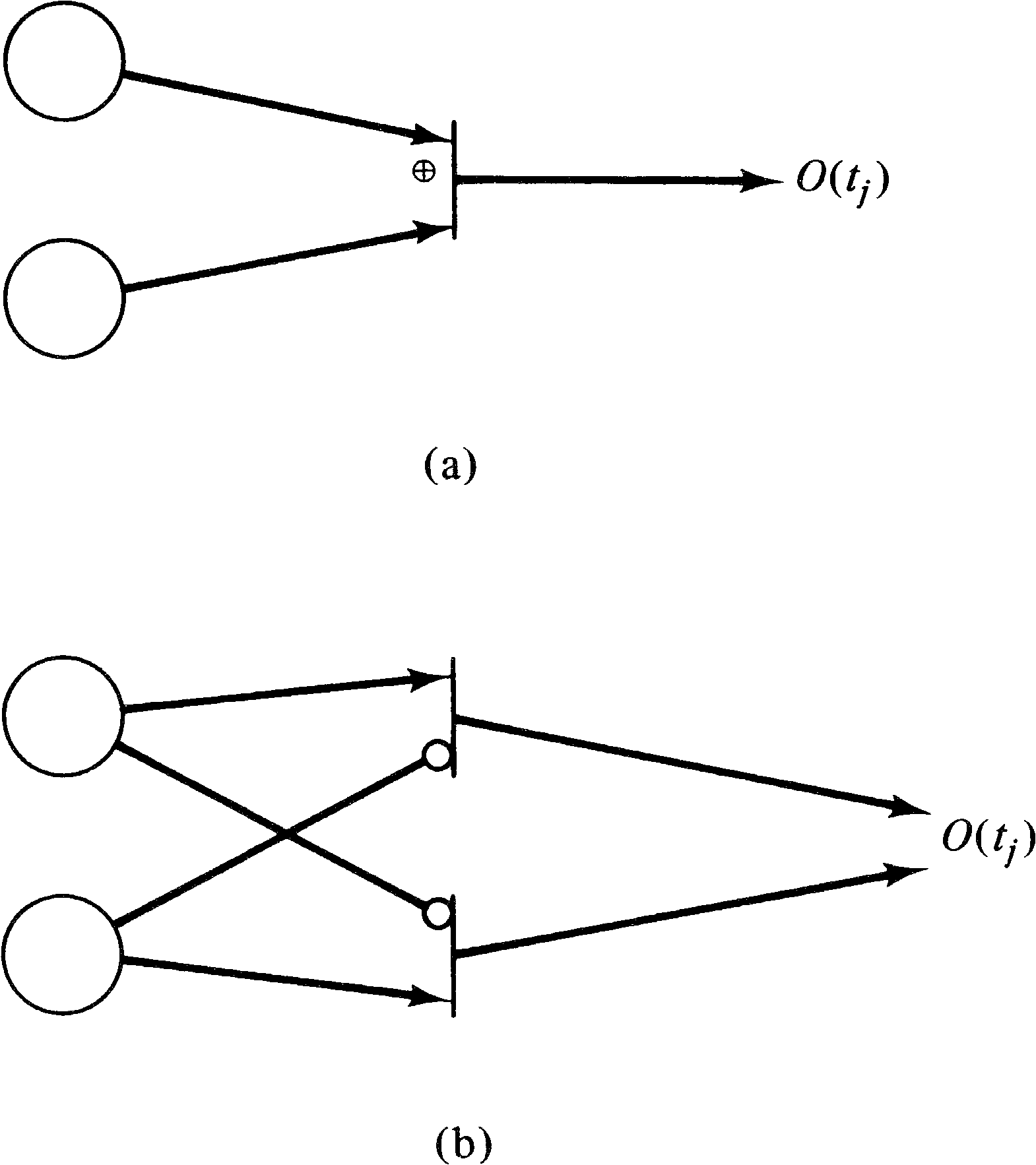
exclusive-OR transition (Figure 7.1). Normally, a Petri net
transition fires when all of its inputs have tokens; this is
called AND logic, since we must have tokens in the
first input and tokens in the second input and
tokens in the third input and so on. The exclusive-OR
transition can fire if and only if exactly one of its inputs
has tokens and all the others have zero tokens. Thus, the
enabling rule is that the first input have a token or the
second input have a token (but not both). When the
transition fires, it removes a token only from the input
with tokens.

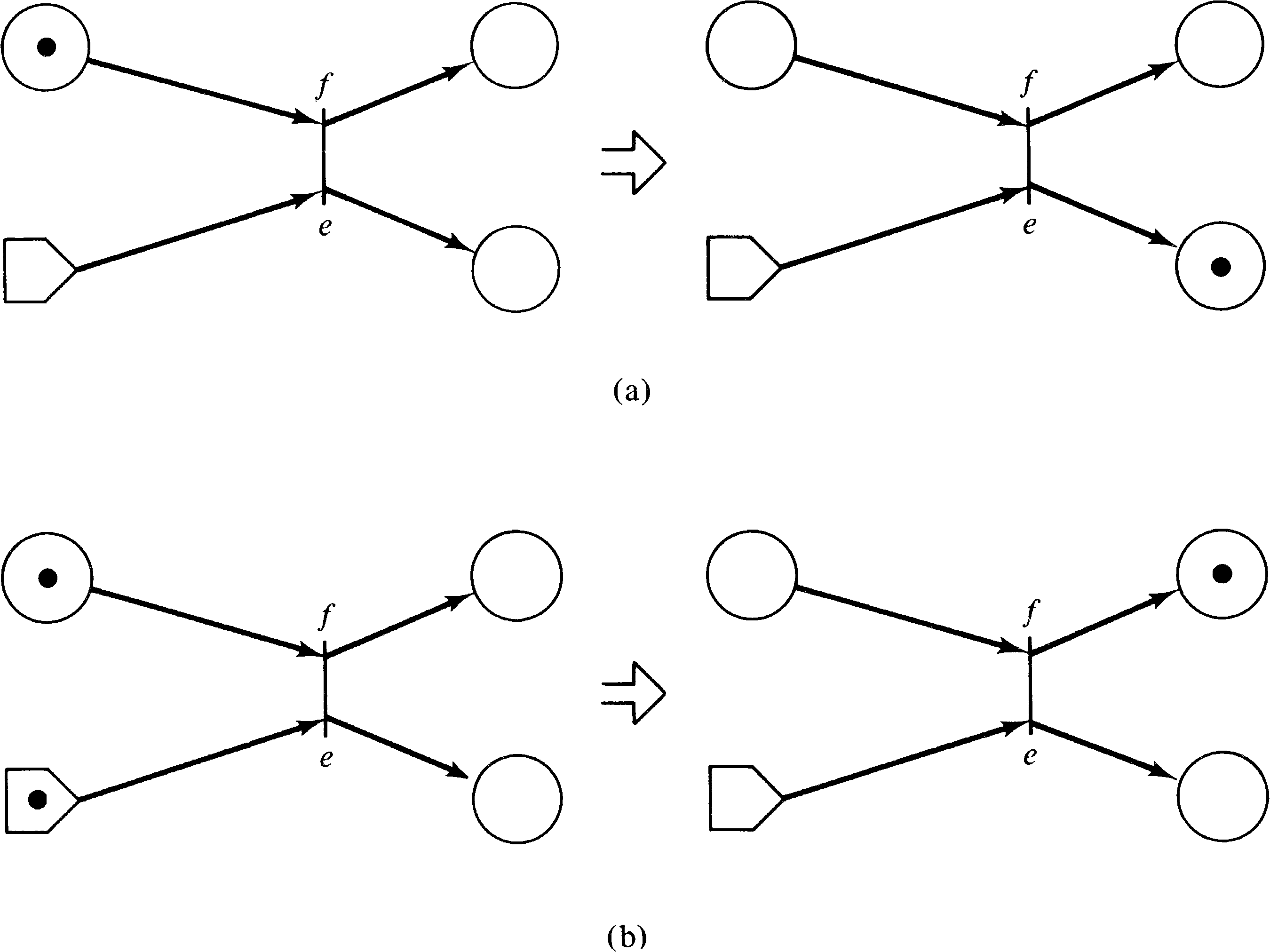
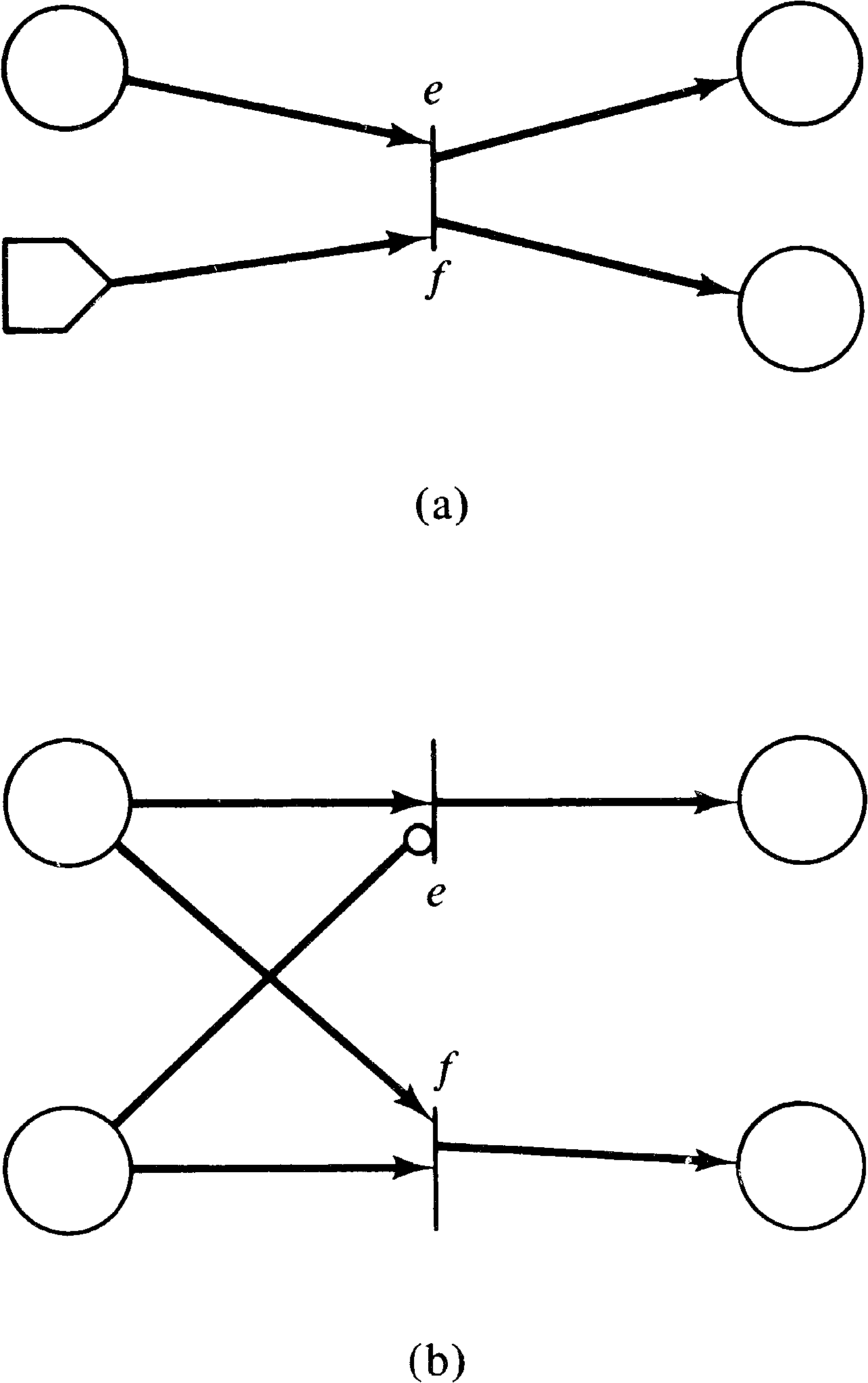
A similar extension was used by Baer in his model of a
compiler [Baer 1973b]. Baer introduced switches (Figure 7.2). A
switch is a special transition with a special input called
the switch input and exactly two outputs (one labeled
e for empty and the other labeled f for full).
A switch transition fires when it is enabled (ignoring the
state of the special switch input). When it fires a token
is put in the output labeled e if the switch input is
empty and a token is put in the output labeled f if
the switch input is full. Thus, firing a switch transition
will result in either one of two markings, depending on
the state of the switch. A token is removed from the switch
input if it had one, so that the switch input is empty after
the switch transition is fired.
These extensions to Petri nets were created for solving specific problems which the researchers encountered in their attempts to model real systems. However, the emphasis of their work was modeling, not the theoretical power of Petri nets, so no attempt was made to show that these extensions were either necessary or sufficient to handle general modeling problems. In fact, in all of these cases, the nets involved were safe, and hence the reachability set is finite, meaning that these nets could be represented by finite state machines, which we have seen (Section 3.3.1) can be easily represented as ordinary Petri nets. Thus, in these cases, these “extensions” were not necessary, merely convenient. We have also seen, in Section 5.3, that many “extensions” to the restricted Petri net model, such as multiple arcs and self-loops, are not in fact extensions but merely convenient.
So the question remains as to what, if any, are the limitations of Petri nets. The answer to this question was found as the result of asking similar questions about Dijkstra's P and V operations on semaphores.
Dijkstra defined his P and V operations on semaphores to facilitate synchronization and communication in systems of cooperating processes [Dijkstra 1968]. A semaphore can be thought of as an integer variable which only takes on nonnegative values. A V operation on a semaphore S increases the value of the semaphore by one, S = S + 1 . A P operation, on the other hand, decrements S by one as long as the result is nonnegative; the process must wait until S can be decremented before it continues. The relationship between semaphores and Petri nets was examined in Section 3.4.8.
Since P and V operations were proposed as the mechanism for solving all synchronization problems between programs, questions naturally arose as to their completeness, that is, their ability to solve all possible coordination problems. Patil [1971] set out to prove that P and V operations are not powerful enough to solve all coordination problems. His approach was quite simple: He created a synchronization problem which cannot be solved with P and V operations. The problem posed was the cigarette smokers' problem.
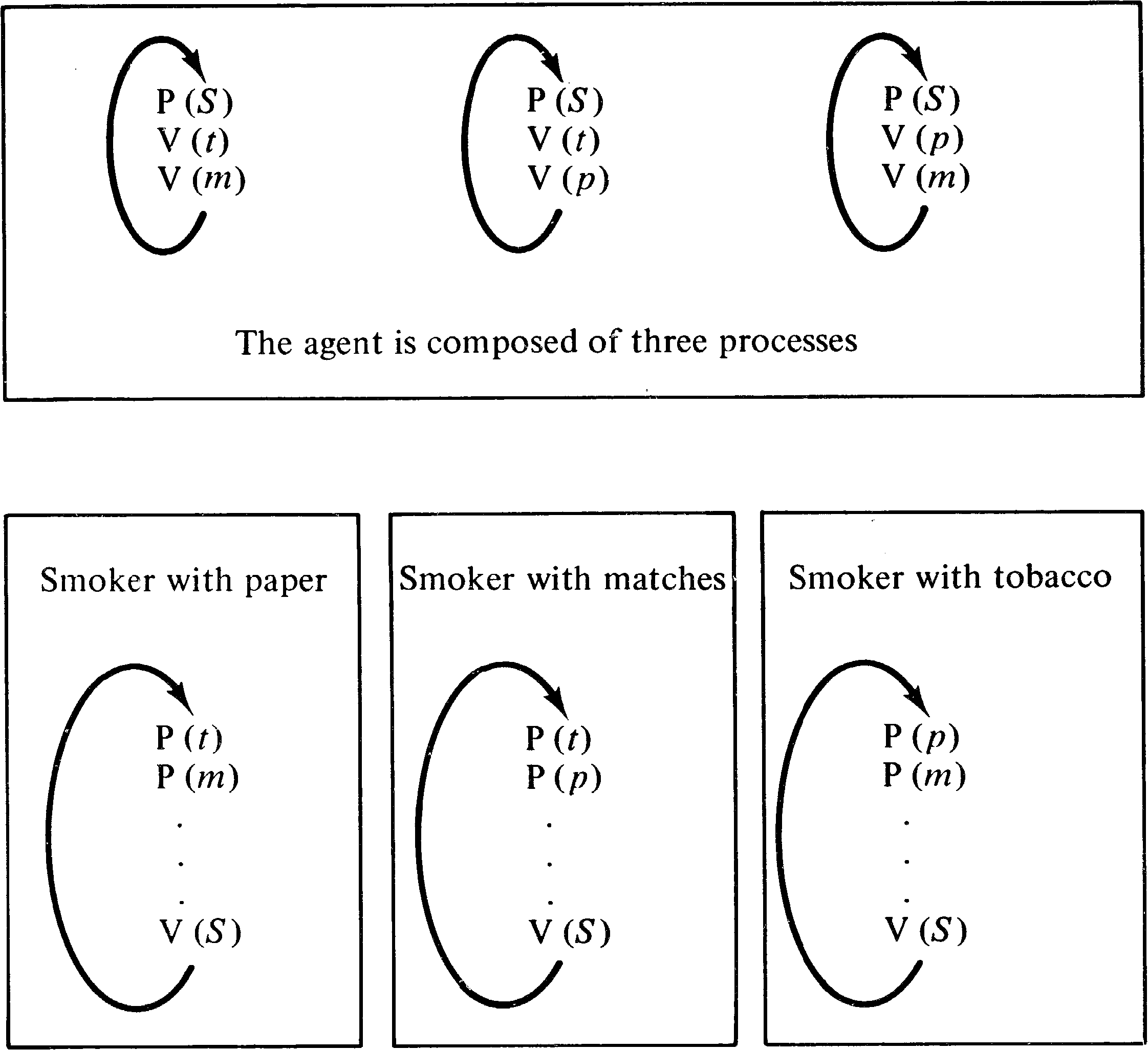
The cigarette smokers' problem consists of (at least) four processes: an agent and three smokers. Each smoker continuously makes a cigarette and smokes it. But to make a cigarette, three ingredients are needed: tobacco, paper, and matches. One of the processes has paper, another tobacco and the third has matches. The agent has an infinite supply of all three. The agent places two of the ingredients on the table. The smoker who has the remaining ingredient can then make and smoke a cigarette, signaling the agent upon completion. The agent then puts out another two of the three ingredients and the cycle repeats.
In terms of semaphores, the problem is posed by associating a semaphore with each ingredient. These semaphores are initially zero. The agent will increment two of the three semaphores by V operations, and then wait on a done semaphore. The appropriate smoker process must decrement the two semaphores (by P operations), make and smoke the cigarette, and increment the done semaphore. The problem is to define the code for the smoker processes to determine which of the three processes should proceed; the agent is fixed and cannot be changed.
Figure 7.3 illustrates the obvious “solution.” The problem
with this “solution” is quite simple: Suppose the agent
puts out tobacco and paper [ V(t); V(p) ]. Then
the smoker with paper may grab the tobacco [ P (t) ] and
the smoker with tobacco may grab the paper [ P (p) ],
resulting in a deadlock.
Patil proved that no sequence of P and V operations can correctly solve this problem. This was shown by proving that all P and V “solutions” can be modeled as Petri nets of a certain kind (each transition has at most two inputs) but that the solution is a Petri net of another kind, and there is no way to convert a net of one kind into a net of the other kind without introducing the danger of deadlock.
There were some problems with Patil's solution -- specifically dealing with arrays of semaphores (see [Parnas 1972]) -- but the concept is correct. Kosaraju [1973] and Agerwala and Flynn [1973] followed up on Patil's work to produce a problem which cannot be solved by P and V operations or by Petri nets. This same limitation had been earlier discovered by Keller [1972].
The problem posed by Kosaraju and Agerwala and Flynn is
quite real. Assume that we have two producer processes and
two consumer processes. One producer process P1 creates
items for the first consumer process C1, and the other
producer P2 produces for the other consumer C2. Items
which are produced but not yet consumed are placed in a
buffer, buffer B1 for (P1, C1 ) and B2 for
(P2, C2 ) . The transmission from the buffers to the
consumers is over a shared channel. The channel can only
transmit one item at a time but can transmit from either
buffer to either consumer. The producers merely put items
into the buffers; the consumers must coordinate the use of
the channel between themselves. The controlling consumer
tells the channel to fetch an item from the appropriate
buffer. This is sketched in Figure 7.4.
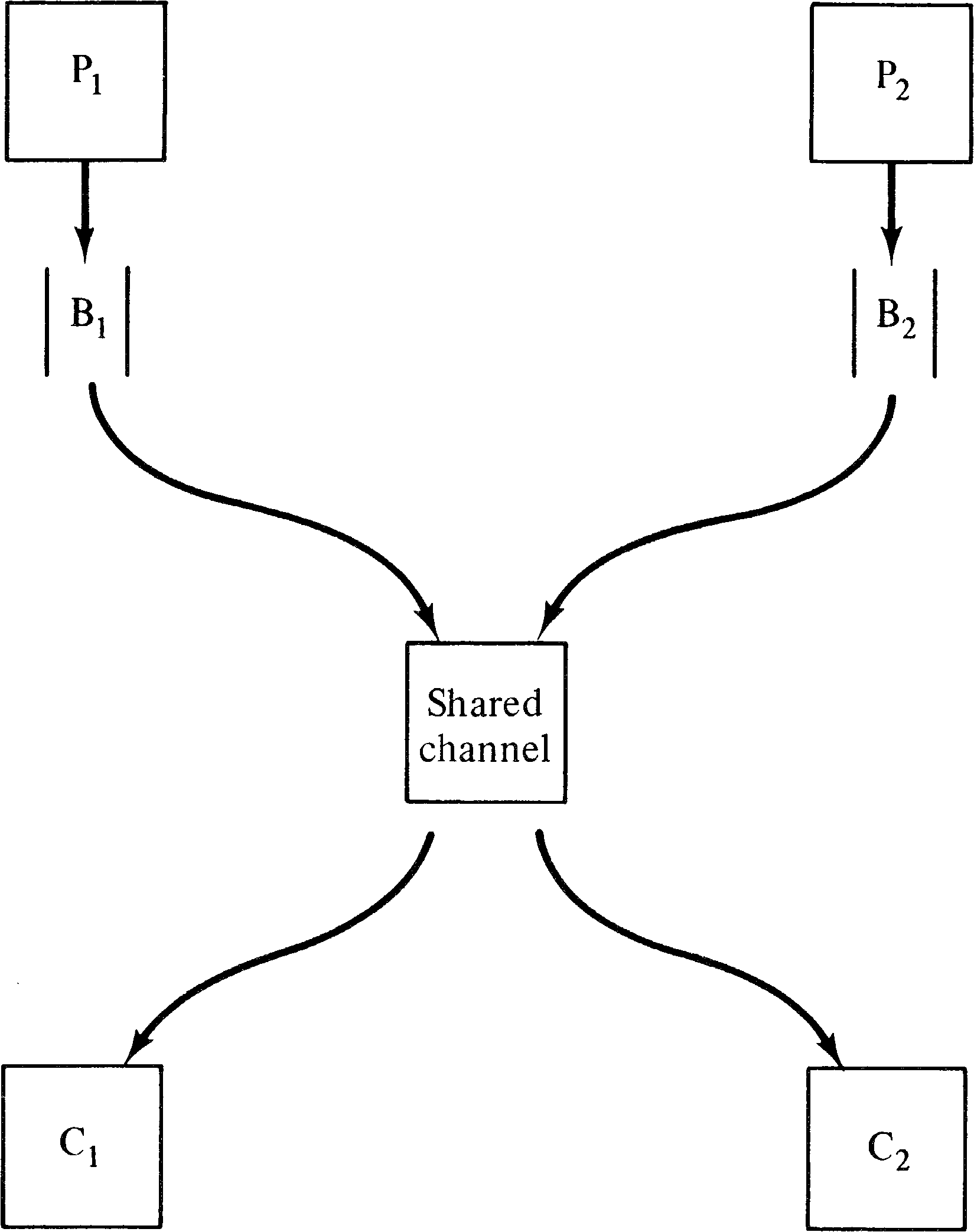
The major problem with this system is the allocation of the channel. The producer/consumer pair (P1, C1 ) are required to have priority over (P2, C2 ) for use of the channel. Specifically, the channel is never to transmit items from buffer B2 to consumer C2 as long as buffer B1 is nonempty. This priority rule prevents this system from being modeled as a Petri net.
The proof is relatively straightforward. Assume that we are in a state μ with items in both buffer B1 and buffer B2. Now, if producer P1 takes a break, then all items from buffer B1 will eventually be transmitted to consumer C1, and buffer B1 will be empty. This will allow an item from buffer B2 to be moved to consumer C2. Thus there exists a path from μ to a state μ′ in which consumer C2 can use the channel. Now, if instead the producer P1 produces an extra k items, then we will be in state μ + k rather than μ . But because of the permissive nature of Petri net firings, the sequence of firings which took us from μ to μ′ will still be enabled and will take us from μ + k to μ′ + k. And since consumer C2 could use the channel in μ′ and Petri nets are permissive, consumer C2 can still use the channel, despite the presence of k items in buffer B1. Thus, the permissive nature of Petri net firings does not allow this priority system to be modeled correctly.
More specifically, the limitation on Petri net modeling is
precisely the inability to test for exactly a specific
marking in an unbounded place and take action on the
outcome of the test. This is commonly stated as an
inability to test for a zero marking in a place, and so this
property is known as zero testing [Keller 1972].
Petri nets cannot test an unbounded place for zero. [If the
place is bounded, zero can be tested. For a bounded place
pi with bound k, we can create a
complement place pi′ such that the
sum μ ( pi ) + μ ( pi′ )
is constant at k for
all reachable markings. This allows us to test if
μ ( pi ) is zero by testing if
μ ( pi′ ) is k.]
Exercises
How does this limitation of Petri net modeling power relate to the extensions of Petri nets which have been suggested? All of the suggested extensions are directed at creating an ability in Petri nets for zero testing.
The simplest extension to Petri nets which allows zero
testing is inhibitor arcs. An inhibitor arc is
illustrated in Figure 7.5. An inhibitor arc from a place
pi to a transition tj has a
small circle rather than an arrowhead at the transition.
This notation is borrowed from switching theory where the
small circle means “not.” The firing rule is changed as
follows: A transition is enabled when tokens are in all of
its (normal) inputs and zero tokens are in all of its
inhibitor inputs. The transition fires by removing tokens
from all of its (normal) inputs.
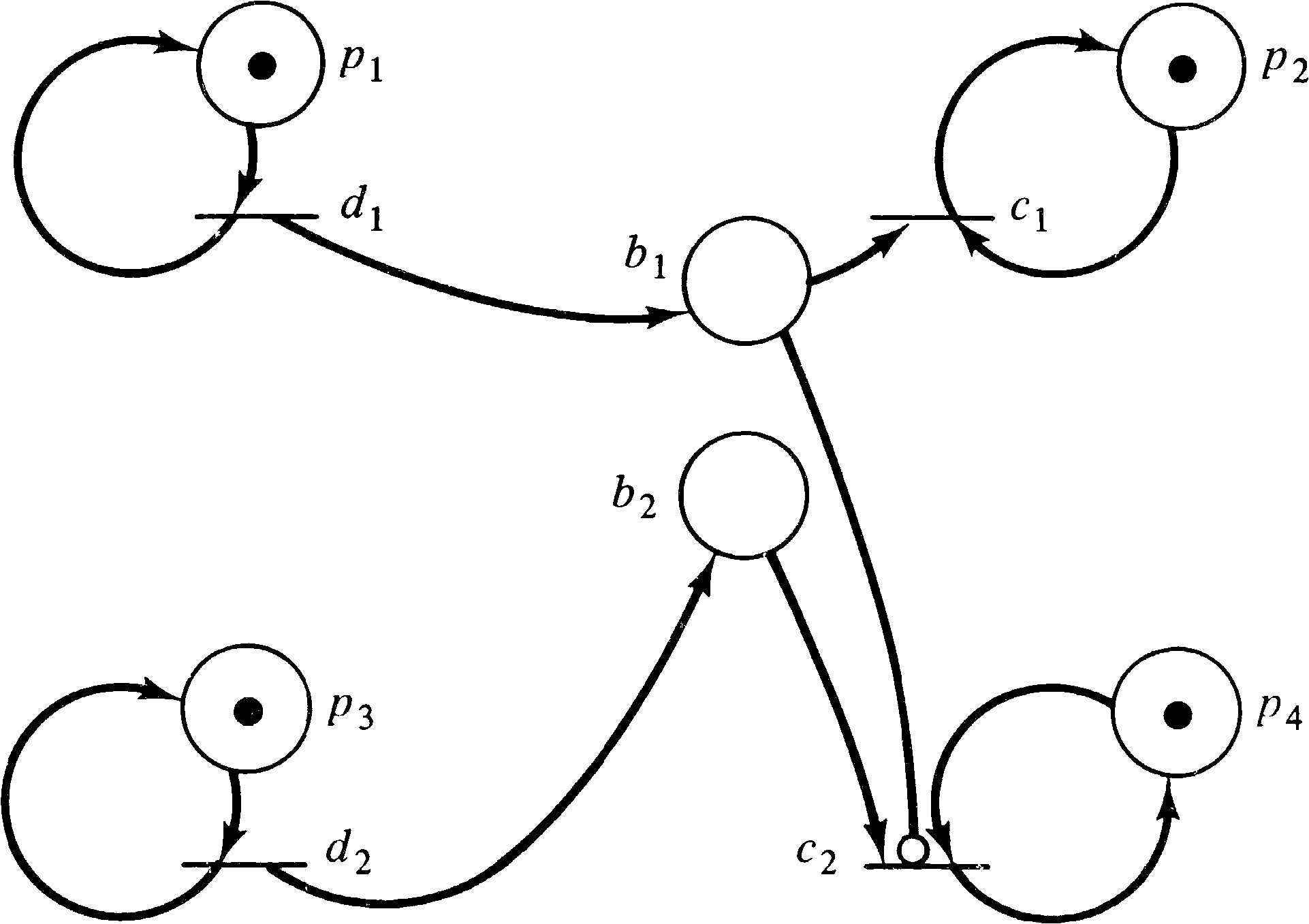
Thus in the extended Petri net of Figure 7.5, transition C2 can fire only if there is a token in b2 and p4 and zero tokens in b1. This net is a solution to the priority shared channel problem which Kosaraju defined to show the limitations of Petri nets.
Petri nets with inhibitor arcs are intuitively the most
direct approach to increasing the modeling power of Petri
nets. It is also the case that all other extensions to
Petri nets which have been suggested either are not true
extensions (that is, they are in fact equivalent to ordinary
Petri nets) or are equivalent to Petri nets with inhibitor
arcs. We discuss several suggested extensions below to
illustrate this point.
7.2.1. Constraints
Constraints were proposed by Patil [1970a] to improve the modeling power of Petri nets. In Patil's context, constraints were only meant to make the modeling easier but not to increase modeling power, because the places in Patil's work were all bounded. However, the definition of constraints is not limited to bounded Petri nets, and for the more general class of Petri nets, they are equivalent to inhibitor arcs.
To show the equivalence of constraints and inhibitor arcs, assume we have a Petri net C = (P, T, I, O) with a constraint Q ⊆ P. We must guarantee that all places in Q are not marked in any reachable marking. The only way this could happen would be for a transition tj to fire putting tokens in those places of the constraint which were not marked before the transition fired. Thus, for each transition tj with output places which are in the constraint, we must guarantee that at least one of the members of the constraint will not be marked after the transition fires. To assure this, we create a new transition tj, k for every place pk in the constraint Q but not in O ( tj ) . The transition tj, k is identical to tj except that it also has an inhibitor arc from pk to tj, k. The effect of firing tj, k is the same as firing tj, and if tj can be fired without violating a constraint, then at least one of the tj, k can fire.
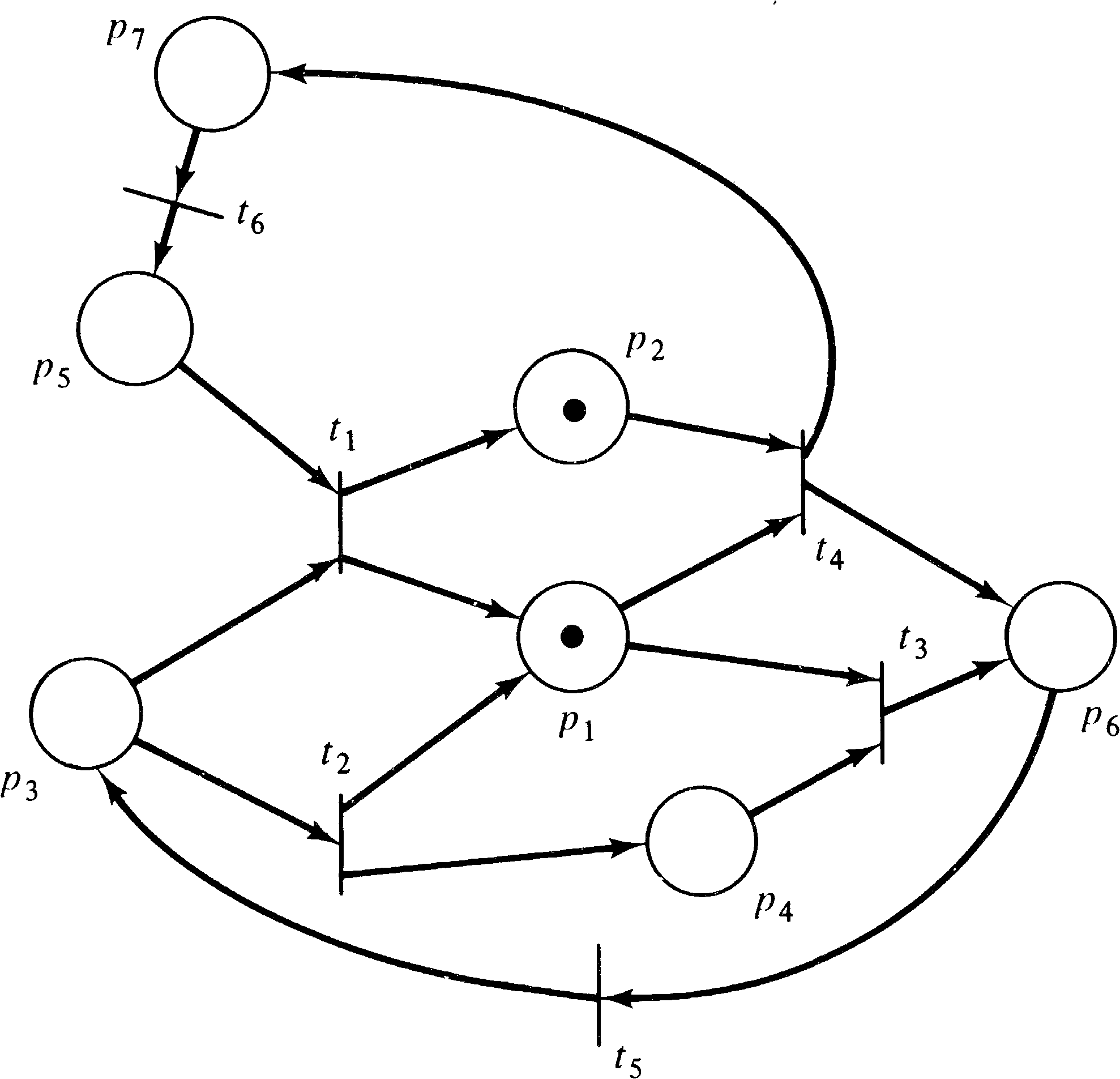
As an example of this construction, consider the Petri net
of Figure 7.6. If we impose the constraint
{ p3, p7 }
(that is, no marking should have p3
and p7 simultaneously marked), then the equivalent
Petri net with inhibitor arcs is shown in Figure 7.7.
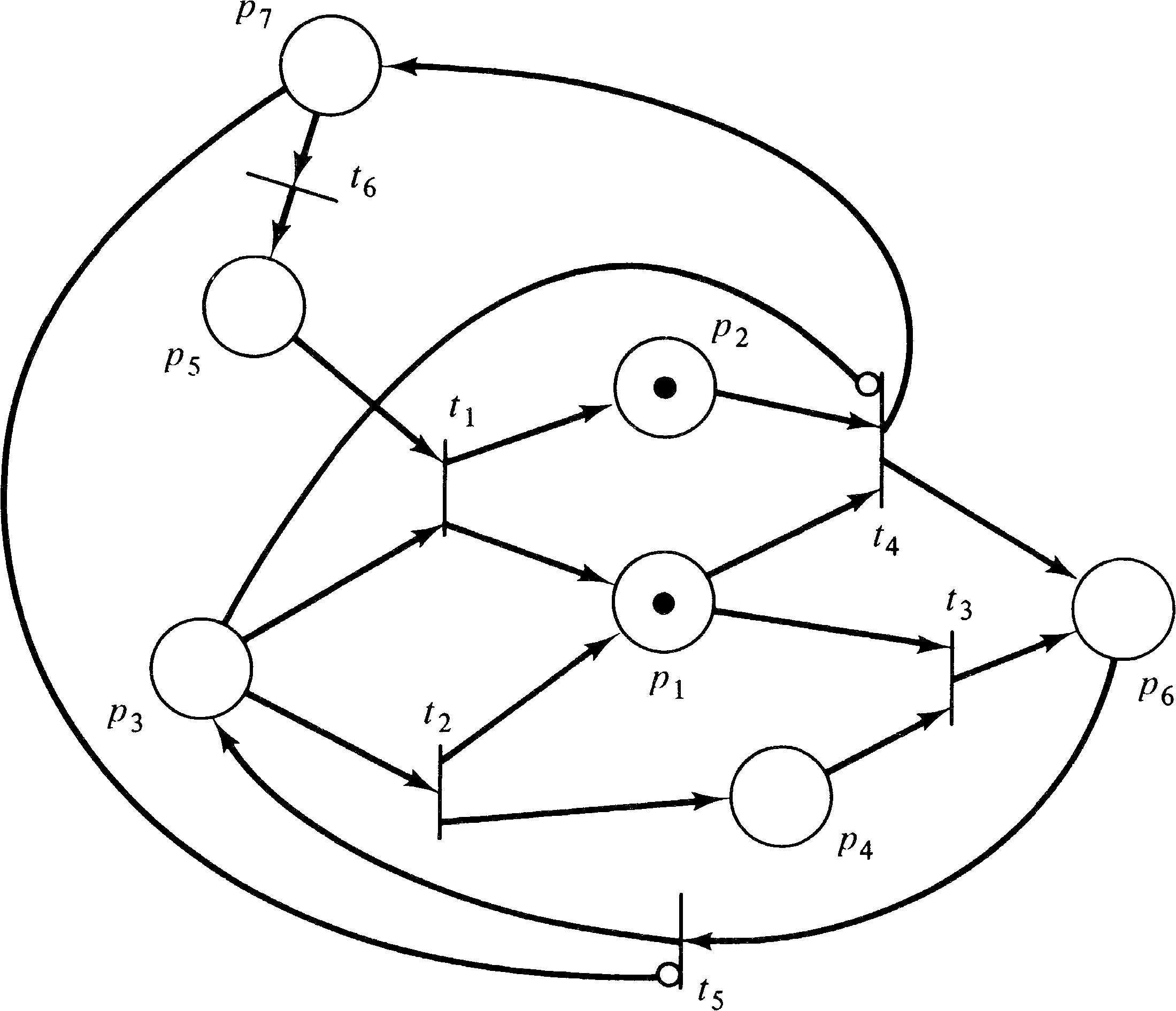
The transformation from inhibitor arcs to constraints is
somewhat more difficult. We cannot simply insist that no
output of a transition can be marked at the same time as an
inhibitor input, since tokens can be placed in the
output by other transitions. We must concentrate on
the transition. This requires splitting each transition
tj into two transitions
tj′ and
tj′′ and a place
pj′ . We define
I ( tj′ ) = I ( tj )
(without the inhibitor arcs) and
O ( tj′′ ) = O ( tj ) .
The place pj′ represents the firing of
tj, so
O ( tj′ ) = { pj′ } = I ( tj′′ ) . This is illustrated in
Figure 7.8. Now, for each place pi which is
an inhibitor input to tj, we define a
constraint { pi, tj′ } .
This assures that the transition cannot fire if the marking
of pi is nonzero.
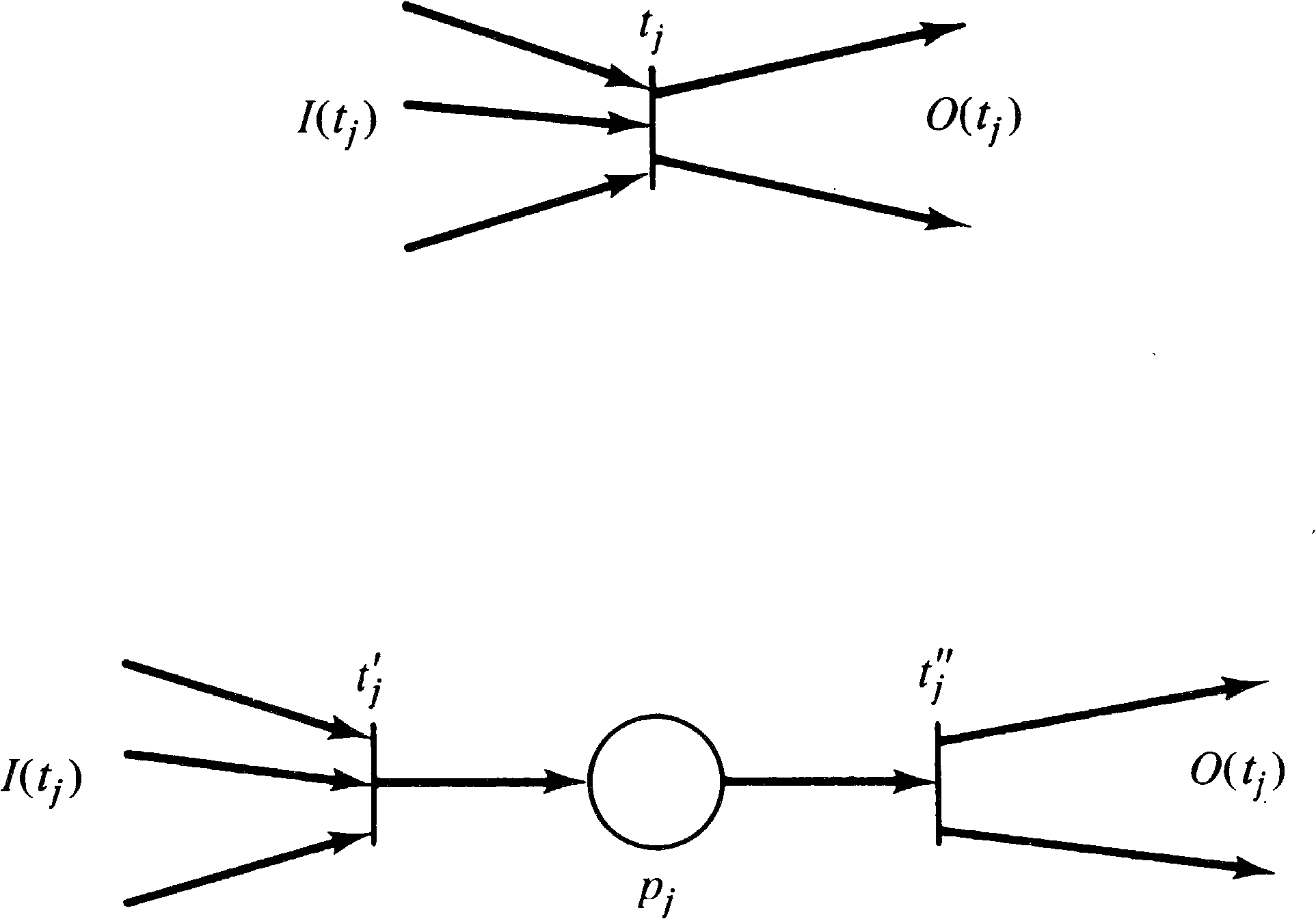
An exclusive-OR transition tj with input
I ( tj ) requires that one and only one of its
inputs be nonzero to enable the transition. This is
equivalent to a set of transitions, one for each element in
I ( tj ) . Each transition has one (normal)
input, and the rest of the inputs are inhibitor arcs. Figure
7.9 gives an example.
Switches can also be easily transformed into inhibitor arcs.
See Figure 7.10.
It is not immediately obvious how inhibitor arcs can be
converted into either switches or exclusive-OR transitions,
but it is certainly the case that they can be.
7.2.3. Other Extensions
Two other major extensions to Petri nets have been suggested. Priorities can be associated with the transition such that if ti and tk are both enabled, then the transition with the highest priority will fire first [Hack 1975c]. Time Petri nets [Merlin 1974] associate with each transition tj two times τ1, j and τ2, j. A transition tj can fire only if it has been enabled for at least time τ1, j, and it must fire before τ2, j if it is enabled. Both of these extensions can be used to test for zero.
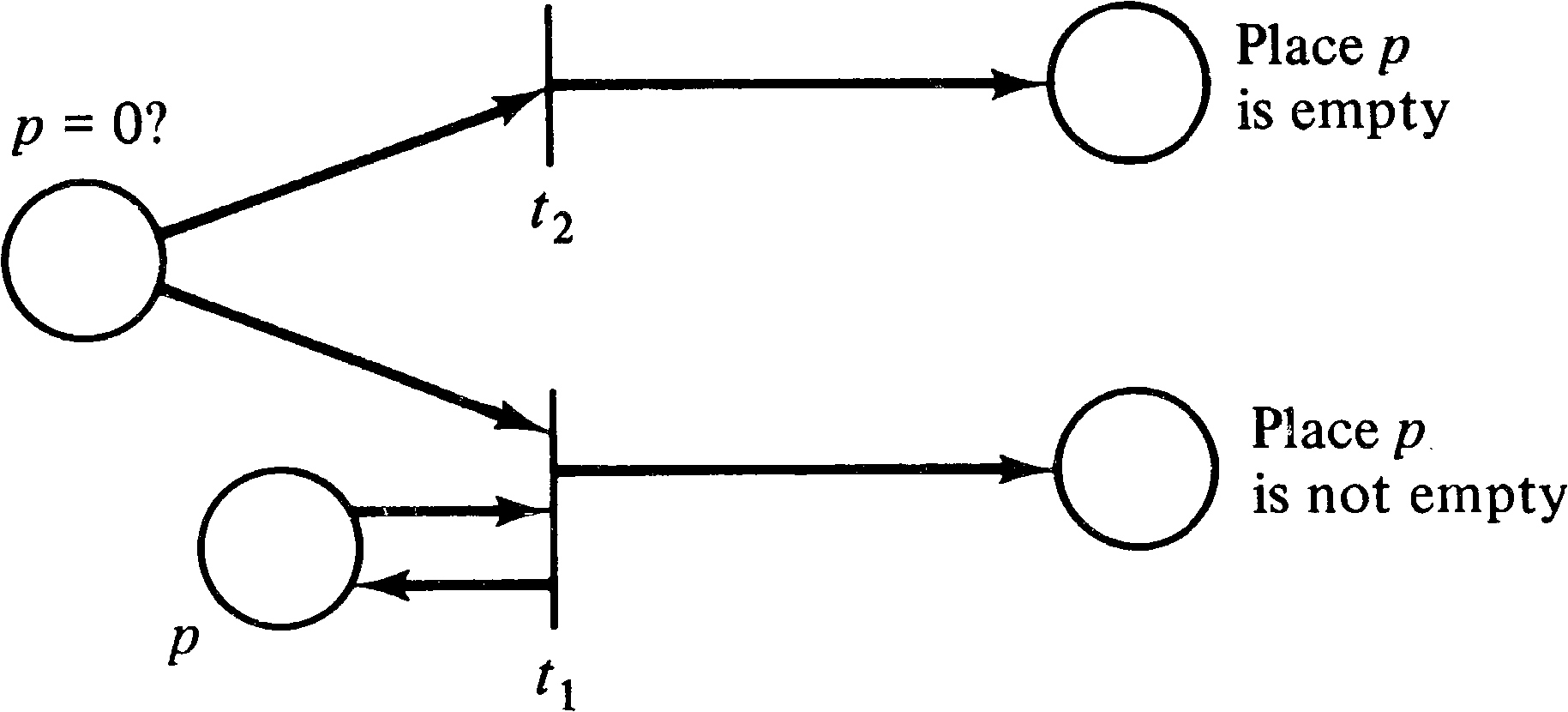
In the case of priorities, we can easily test if a place
pi is zero. This is shown in Figure 7.11.
If we put a token into place pi = 0 ? and
define the priority of transition t1 to be higher
than the priority of transition t2, then we will
get a token in one of the two places at the right depending
on the marking of place pi. This results
from the fact that transition t1 can fire only if
it is enabled, and it is enabled only if place
pi has a token. If t1 cannot fire
because pi is empty, then, and only then,
will transition t2 fire.
Hack has shown complete constructions for converting Petri
nets with priorities to Petri nets with inhibitor arcs and
vice versa [Hack 1975c]. Time Petri nets can also test a
place for zero by simulating priorities. If we have two
transitions tj and tk and we
set τ2, j < τ1, k, then transition
tj has priority over transition
tk since tj must fire
(if it is enabled)
before tk would be allowed to fire.
7.3. Extended Petri Nets and Register Machines
We have shown that the suggested extensions to the Petri net model all allow a place to be tested for zero. How is this important to the decision power of a Petri net? Does it affect our ability to analyze Petri nets?
Zero testing decreases the decision power of Petri nets. Agerwala [1974a], Hack [1975c], Thomas [1976], and others have shown that adding the ability to test for zero to a Petri net model allows a Petri net to simulate a Turing machine. Thus a Petri net with zero testing, produces a modeling scheme which can model any system. Also, however, almost all analysis questions for Petri nets become undecidable, since they are undecidable for Turing machines.
The proof of the equivalence of extended Petri nets and Turing machines is relatively simple. It is easiest to give in terms of the register machines of Shepardson and Sturgis [1963] or the program machines of Minsky [1967].
A register machine is a computer-like machine with a number of registers which are used to store arbitrarily large numbers. A program is written to manipulate the registers. The program is a sequence of instructions such as “increase register n by 1,” “decrease register n by 1 (only if register n is not 0),” “jump to statement s if register n is not zero,” and so on. For example, the following is a program to add the contents of register 2 to register 1.
Shepardson and Sturgis have shown that a register machine with the following instructions is equivalent to a Turing machine.
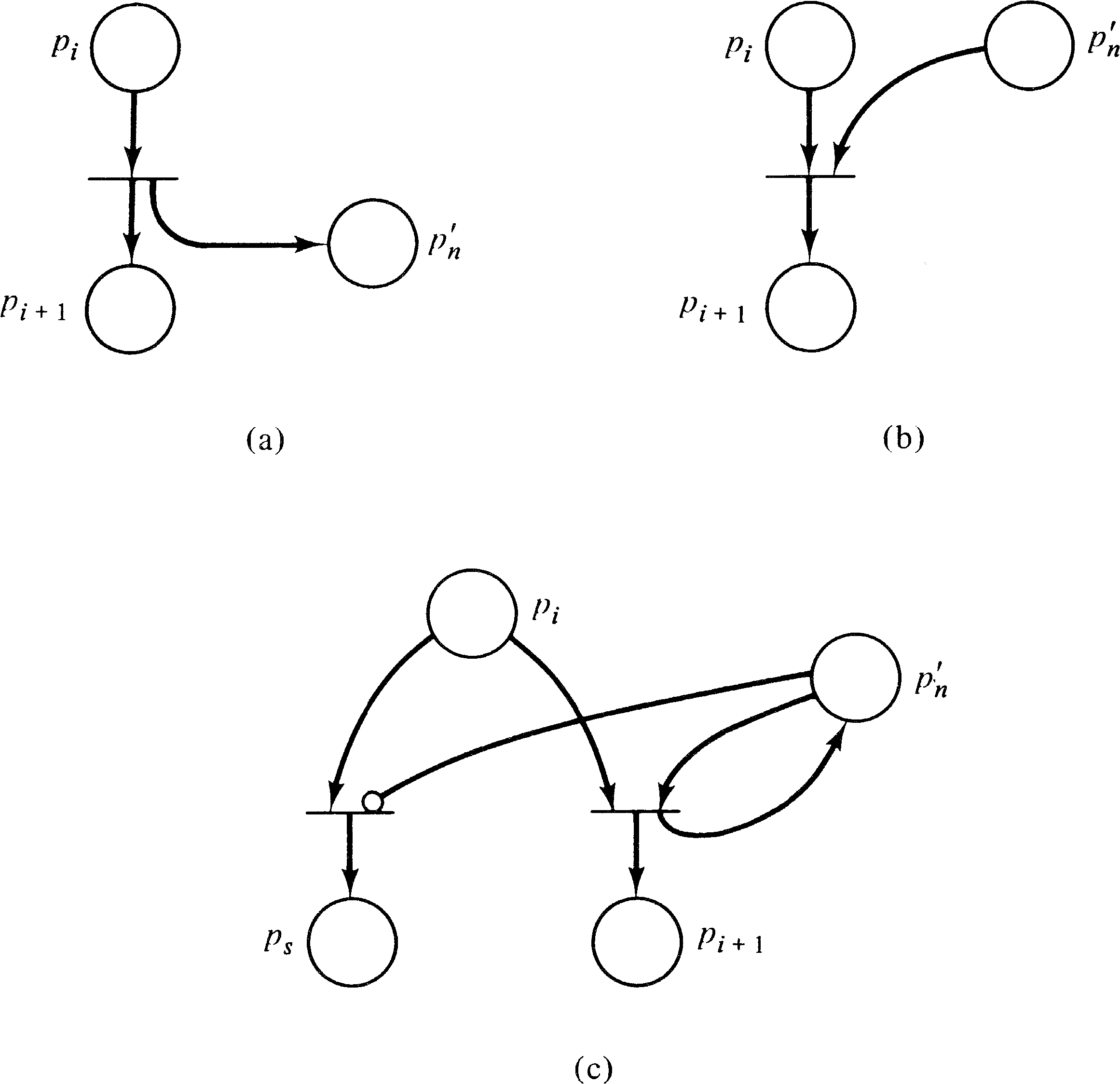
To represent a register machine as an extended Petri net, we
represent the n registers used in a program by n
places, p1′, p2′, …, pn′ . We also use s + 1 places to
represent the position of the program counter either before
statement 1 (the initial marking) or after statement
i, for i = 1, …, s, in a program with
s statements. Each instruction in the program is
represented by a transition. Figure 7.12 shows how each of
the three instructions above would be represented as a
transition in an extended Petri net. This shows that a
register machine can be converted into an extended Petri
net and therefore that an extended Petri net is equivalent
to a Turing machine. This equivalence to Turing machines
destroys any hope of being able to analyze extended Petri
nets. However, it does prove that extended Petri nets can
model any system (or at least any computable system). Thus
we see that an increase in modeling power, in this case,
results in a definite decrease in decision power.
Also notice that the key point in the proof of equivalence of extended Petri nets and register machines and Turing machines is the ability to test a single place for zero. Thus, all of the extensions which have been suggested -- constraints, exclusive-OR transitions, switches, priorities, timings, and inhibitor arcs -- extend the Petri net model to the level of Turing machines.
There have been other suggestions for extensions which do not raise Petri nets to the level of Turing machines. Self-loops and multiple input and output arcs were first suggested as extensions but, as seen in Section 5.3, are in fact equivalent to restricted Petri nets. Similarly, allowing inclusive-OR inputs, inclusive-OR outputs, or exclusive-OR outputs would not increase the modeling power of Petri nets.
In general, it seems that any extension which does not allow
zero testing will not actually increase the modeling power
(or decrease the decision power) of Petri nets but merely
result in another equivalent formulation of the basic Petri
net model. (Modeling convenience may be increased.)
At the same time, any extension which does allow zero
testing will increase the modeling power to the level of
Turing machines and decrease decision power to zero. Thus
Petri net extensions would seem to have few practical
advantages for analysis.
7.4. Subclasses of Petri Nets
The objective of extending Petri nets is to increase their modeling power; an unfortunate side effect is that the decision power of extended Petri nets is greatly reduced. The decision power of normal Petri nets is of questionable value anyway due to its complexity and expense. (Remember the results of Section 5.8 on the complexity of the reachability and boundedness problems.) This has resulted in some investigations of subclasses of Petri nets. The objective of these studies is to determine reasonable structural restrictions on Petri nets which will increase the decision power of the restricted Petri net models while not overly restricting modeling power.
Much can be done with Petri net subclasses. The goal of this part of Petri net research is quite simple: Define a subclass of Petri nets which can model a large class of systems (all or almost all interesting ones) and yet still has simple analysis procedures (at least for the interesting problems). It is also necessary that there exist a simple test for determining if a Petri net is a member of the defined subclass. The subclasses which have been defined are all syntactic or structural subclasses; one can easily examine a Petri net structure to determine if it is a member of the specified subclass. This is in distinction to subclasses which might be defined according to dynamic properties, such as, for example, persistent Petri nets [Landweber and Robertson 1975] or bounded Petri nets. These subclasses might have very nice properties, but it may be quite difficult to determine if an arbitrary given Petri net is a persistent or bounded Petri net.
Only two major subclasses of the Petri net model have been
widely studied: state machines
and marked graphs. In addition,
Hack [1972] has studied a subclass
called free-choice Petri nets and has suggested that
another subclass, simple Petri nets, might have good
decision properties. We present each of these classes and
indicate their major properties, advantages, and
disadvantages.
7.4.1. State Machines
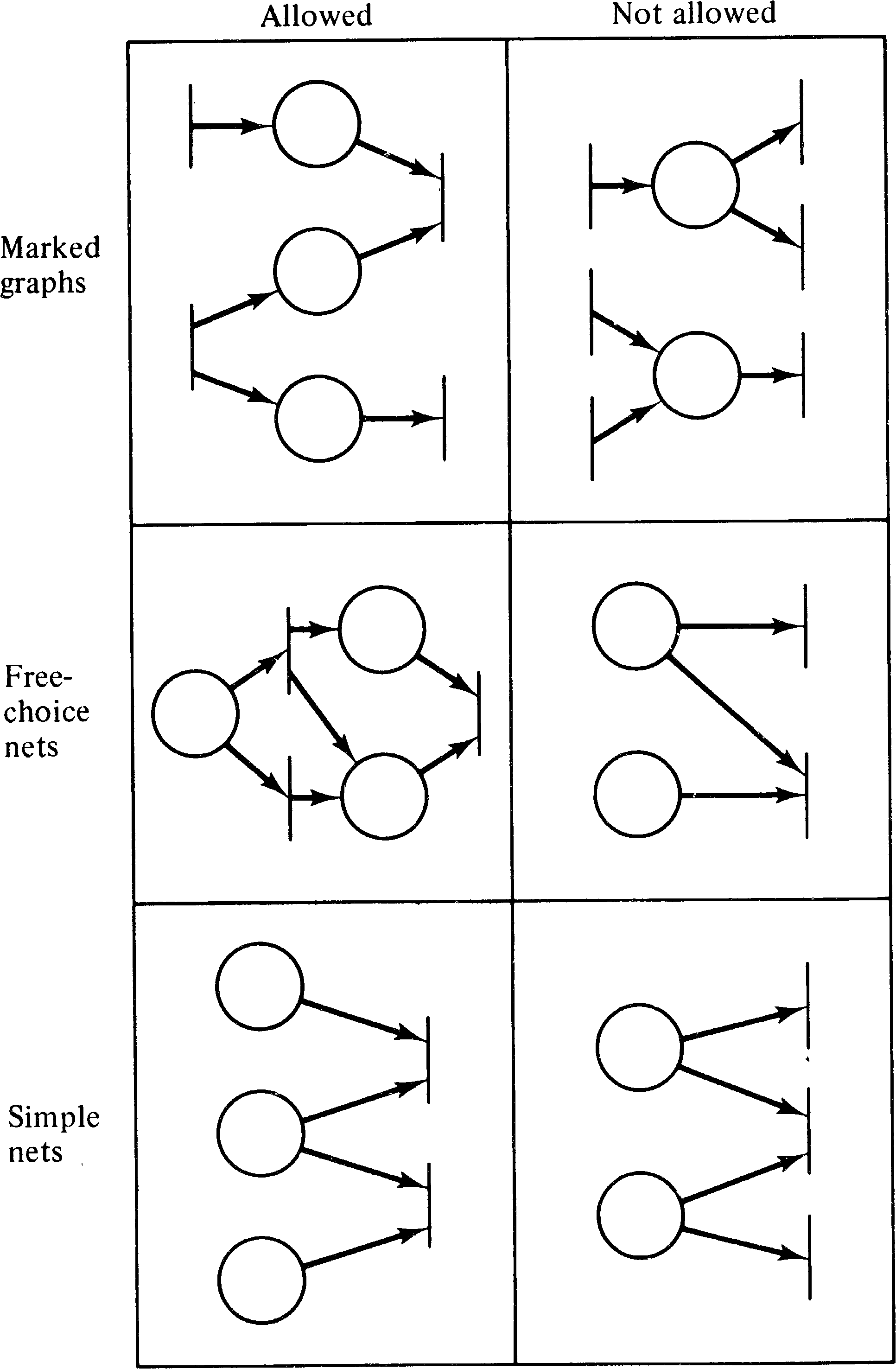
A state machine is a Petri net in which each transition is restricted to having exactly one input and one output.
Several properties of state machines are immediately
obvious. First, a state machine is strictly conservative.
This means that the number of tokens in the state machine
never changes, resulting in a finite system. This implies
that the reachability tree for a state machine is finite,
and hence all analysis questions are decidable for state
machines. In fact, a state machine is equivalent to the
finite state machine automata of automata and formal
language theory (see Section 3.3.1). Thus, these models are
of limited interest despite their high decision power, due
to the limited modeling power of finite state machines.
7.4.2. Marked Graphs
Another subclass of Petri nets which is often mentioned in the literature is the class of marked graphs. A marked graph is a Petri net in which each place is an input for exactly one transition and an output of exactly one transition. Alternatively, we can say that each place has exactly one input and one output.
Marked graphs are duals of state machines, in the graph-theoretic sense of the word, since transitions have one input and one output in state machines, while places have one input and one output in marked graphs. They are also duals from the point of view of modeling. A state machine can easily represent conflicts by a place with several outputs but cannot model the creation and destruction of tokens needed to model concurrency or the waiting which characterizes synchronization. Marked graphs, on the other hand, can model concurrency and synchronization but cannot model conflict or data-dependent decisions.
The properties which have been investigated for marked graphs have been liveness, safeness, and reachability. In the investigation of these properties, the major structural parts of a marked graph of interest are its cycles. A cycle in a marked graph is a sequence of transitions tj1 tj2 tj3... tjk such that for each tjr and tjr + 1 in the sequence there is a place pir with pir ∈ O ( tjr ) and pir ∈ I ( tjr + 1 ) and tj1 = tjk. A cycle is thus a closed path from a transition back to that same transition.
For example, in the marked graph of Figure 7.13, the
sequence t1 t2 t1 is a cycle,
as are t4 t3 t4 and
t2 t4 t3 t1 t2.
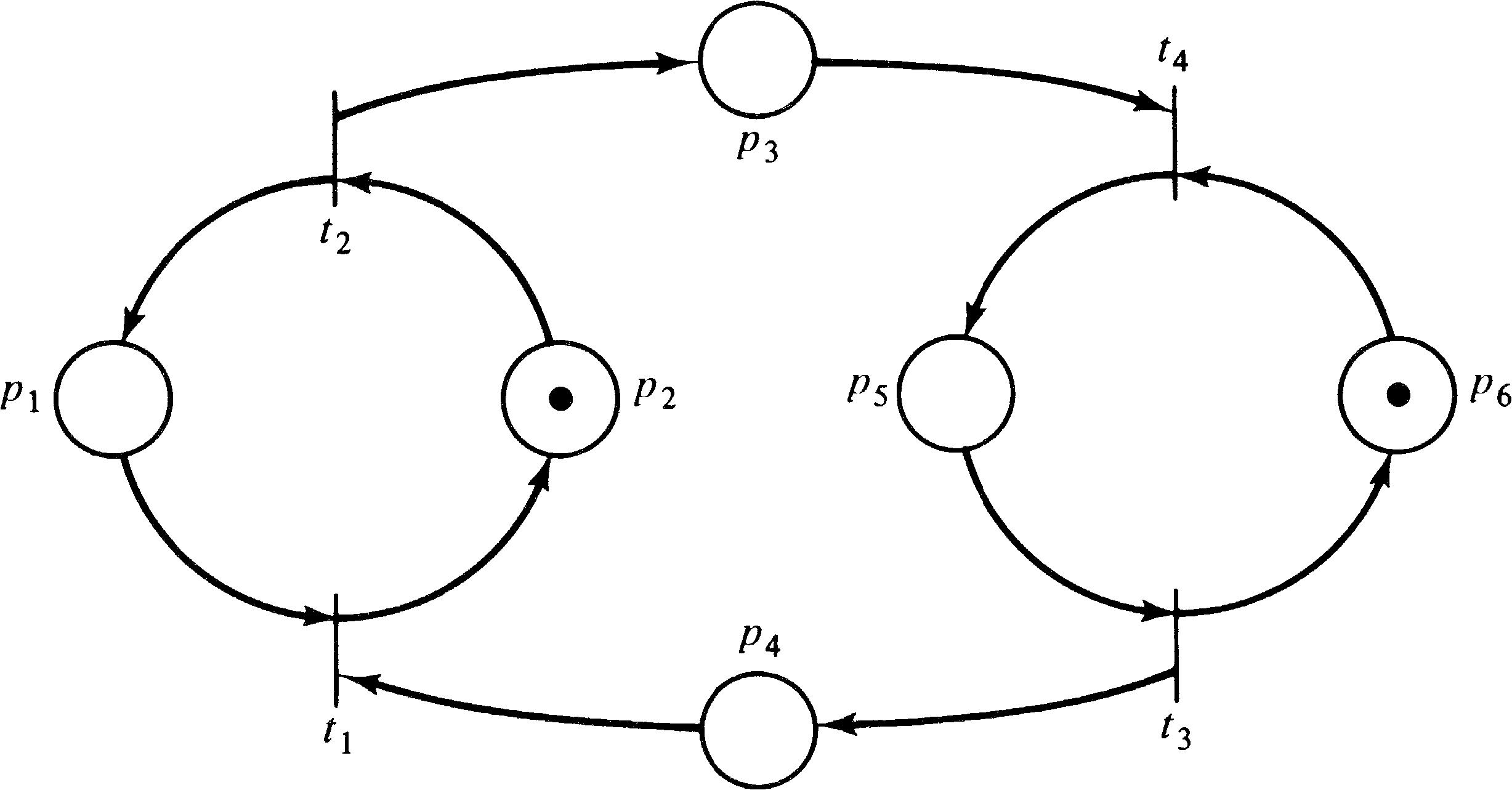
The importance of cycles for marked graphs derives from the following theorem.
Hack, in his Master's thesis at M.I.T. [Hack 1972], defined and investigated one such subclass of Petri nets, the free-choice Petri nets. This subclass allows both the conflicts of state machines and the concurrency of marked graphs but in a more restricted manner than the general Petri net model.
The importance of this definition is the way in which it allows controlled conflict. Conflict occurs only when one place is an input to several transitions. By the definition of free-choice Petri nets, if a place is an input to several transitions (potential conflict), then it is the only input for all of these transitions. Hence either all of these conflicting transitions are simultaneously enabled, or none of them are. This allows the choice (conflict resolution) as to which transition is to fire to be made freely; the presence of other tokens in other places is not involved in the choice as to which transition fires.
This restricted form of conflict allowed Hack [1972] to prove necessary and sufficient conditions for a marked free-choice Petri net to be live and safe. The liveness condition is related to the markings of traps and deadlocks in the net. A trap is a set of places such that every transition which inputs from one of these places also outputs to one of these places. This means that once any of the places in a trap has a token there will always be a token in one of the places of the trap. Firing transitions may move the token between places but cannot remove a token from the trap. A deadlock is a set of places such that every transition which outputs to one of the places in the deadlock also inputs from one of these places. This means that once all of the places in the deadlock become unmarked, the entire set of places will always be unmarked; no transition can place a token in the deadlock because there is no token in the deadlock to enable a transition which outputs to a place in the deadlock.
Hack proved that a necessary and sufficient condition for liveness in a marked free-choice Petri net is that every deadlock contain a marked trap. This theorem was based on work by Commoner [Commoner 1972; Hack 1972]. Necessary and sufficient conditions for safeness involve showing that the free-choice Petri net is covered by a union of state machines. Details can be found in [Hack 1972].
Unfortunately, no further work has been done on free-choice
Petri nets, and so properties of free-choice Petri nets with
respect to reachability, equivalence, containment, languages,
and so on have not been considered.
7.4.4. Simple Petri Nets
Hack has also defined one other subclass of Petri nets
called simple Petri nets [Hack 1972]. Simple nets
require that each transition have at most one input place
which is shared with another transition and so also serve
to restrict the manner in which conflicts can occur. No
investigation has been made into the properties of this
subclass of Petri nets.
The proof by Patil [1971] that P /V systems cannot solve all synchronization problems and the counterproof by Parnas [1972] are short and interesting. They led to the proofs of Kosaraju [1973] and Agerwala and Flynn [1973] that Petri nets cannot model all concurrent systems. These results led Agerwala to investigate what is needed in a model which can model all systems [Agerwala 1974a; Agerwala 1974b].
The major work on restricted Petri net models is in the
early [Holt et al. 1968] and [Commoner et al. 1971] and the later
[Hack 1972]. Some work has continued on marked graphs
[Izbicki 1973; Murata 1977b], but
little has been done on the other models.
Some encouraging results have been obtained in [Crespi-Reghizzi
and Mandrioli 1975] and [Landweber and Robertson 1975] for
conflict-free Petri nets in which | O ( tj ) | = 1 .
Reachability and liveness are decidable for conflict-free nets.
7.6. Topics for Further Study
| Home | Comments? |