Chapter 6. Petri Net Languages

The discussions of Chapters 4 and 5 have concentrated on problems related to the reachability problem, dealing mainly with problems of reachable markings. A related but quite different approach is to focus not on what markings are reachable but rather on how we reach them. The primary object of interest is then the transition and particularly the sequences of transitions which lead us from one marking to another in a Petri net.

A sequence of transitions is a string, and a set of strings is a language. Thus, in this chapter, we concentrate on the languages defined by Petri nets and their properties.

6.1. Motivation

Petri nets are being developed for two major reasons: (1) the description of proposed or existing systems and (2) the analysis of systems which can be modeled by a Petri net description. The analysis of a Petri net attempts to determine the properties of the net and the system which it models. One of the most important properties of a system is the set of actions which can occur. The set of all possible sequences of actions characterizes the system.

In a Petri net, actions are modeled by transitions, and the occurrence of an action is modeled by the firing of a transition. Sequences of actions are modeled by sequences of transitions. Thus the set of allowable transition sequences characterizes a Petri net and (to the degree that the Petri net correctly models a system) the modeled system.

These sequences of transitions can be of extreme importance in using Petri nets. Assume that a new system has been designed to replace an existing one. The behavior of the new system is to be identical to the old system (but the new system is cheaper, faster, easier to repair, or something). If both systems are modeled as Petri nets, then the behaviors of these two nets should be identical, and so their languages should be equal. Two Petri nets are equivalent if their languages are equal. This provides a formal basis for stating the equivalence of two systems.

A particular instance in which equivalence is important is optimization. Optimizing a Petri net involves creating a new Petri net which is equivalent (languages are equal) but for which the new net is “better” than the old one (for some definition of better). For example, if a Petri net is to be directly implemented in hardware, then a Petri net with fewer places, transitions, and arcs would be less expensive to build, since it has fewer components. Thus one optimization problem might be to reduce | P | + | T | without changing the behavior of the net.

For purposes of optimization, a set of language-preserving transformations might be useful. If a transformation applied to a Petri net produces a new Petri net with the same language, then it is language preserving. An optimal Petri net can be produced by applying language-preserving transformations to a nonoptimal Petri net. Practical use of a Petri-net-based system for modeling and analysis would require a collection of language-preserving transformations.

Petri net languages can also be useful for analysis of Petri nets. Techniques have been developed in Chapter 4 for determining specific properties of Petri nets, such as safeness, boundedness, conservation, liveness, reachability, and coverability. Although these are important (and difficult) properties to establish, they are not the only properties for which a Petri net might be analyzed. It may be necessary to establish the correctness of a modeled system by showing that system-specific properties are satisfied. Thus, either new techniques must be developed for each new property, or a general analysis technique for Petri nets is needed.

A large class of questions can be posed in terms of the sequences of actions which are possible in the system. If we define the set of possible sequences of actions as the language of the system, then we can analyze the system by analyzing the language of the system. Now problems may be answered by considering the emptiness question (Will any sequence get me from here to there?) or the membership question (Is a sequence of this form possible?). This may provide us with a general technique for analyzing arbitrary systems for system-specific properties. Riddle [1972] has investigated analysis based on the language of the modeled system.

Another use of Petri net languages would be in the specification and automatic synthesis of Petri nets. If the behavior which is desired can be specified as a language, then it may be possible to automatically synthesize a Petri net whose language is the specified language. This Petri net can be used as a controller, guaranteeing that all and only the sequences specified are possible. Path expressions [Lauer and Campbell 1974] have been developed to define allowable sequences of actions. Techniques have been developed for automatically creating a Petri net from a path expression.

Another motivation for the study of Petri net languages comes from a desire to determine decidability results for Petri nets. The decidability of many properties of Petri nets is unknown. The decidability of a few basic questions for Petri nets, such as reachability, is the object of much current research. One area in which decidability questions have been considered is formal language theory. By consideration of the languages of Petri nets, the concepts and techniques of formal language theory may be brought to bear on the problems of Petri nets. This may produce new results concerning Petri nets and their decidability questions. It is also possible to use Petri net methods to obtain new useful results about formal languages.

6.2. Related Formal Language Theory Concepts

The Petri net language theory which has developed so far is similar to development of other parts of formal language theory. Several books present the classical theory of formal languages [Hopcroft and Ullman 1969; Salomaa 1973; Ginsburg 1966]. Many of the basic concepts of Petri net language theory have been borrowed from the classical theory of formal languages.

An alphabet is a finite set of symbols. A string is any sequence of finite length of symbols from the alphabet. The null or empty string λ is the string of no symbols and zero length. If Σ is an alphabet, then Σ^* is the set of all strings of symbols from Σ, including the empty string. Σ⁺ is the set of all nonempty strings over an alphabet Σ . Σ^* = Σ⁺ ∪ { λ } .

A language is a set of strings over an alphabet. Languages may in general be infinite; thus representing the language is a problem. Two approaches have been developed for representing languages. One approach is to define a machine which when executed generates a string from the language, and all strings of the language are generated by some execution. Alternatively, a grammar may be defined which specifies how to generate a string of a language by successively applying the productions of the grammar.

Restrictions on the forms of the machines or grammars which generate the languages define classes of languages. The traditional classes of languages are regular, context-free, context-sensitive, and type-0 languages, corresponding to finite state machines, pushdown automata, linear bounded automata, and Turing machines. Each of these classes of languages is generated by the appropriate class of automata. This provides an excellent means of linking Petri net theory to formal language theory: We define the class of Petri net languages as the class of languages generated by Petri nets. The details of the definition should be similar to the details for any of the other classes of languages.

As an example, let us consider finite state machines and regular expressions. A finite state machine C is a five-tuple ( Q, δ, Σ, s, F ), where Q is a finite set of states, Σ is an alphabet of symbols, δ: Q ⨯ Σ → Q is a next state function, s ∈ Q is the start state, and F ⊆ Q is a finite set of final states. The next state function δ is extended to a function from Q ⨯ Σ^* to Q in the natural way. The language L ( C ) generated by the finite state machine is the set of strings over Σ defined by

With each finite state machine is associated a language, and the class of all languages which can be generated by finite state machines is called the class of regular languages. The language of a finite state machine is a characterizing feature of the machine. If two finite state machines have the same language, they are equivalent.

6.3. Definitions of Petri Net Languages

The same basic concepts used to produce a regular language from a finite state machine can be applied to Petri nets to produce a theory of Petri net languages. In addition to the Petri net structure defined by the sets of places and transitions (which correspond roughly to the state set and next-state function of the finite state machine), it is necessary to define an initial state, an alphabet, and a set of final states. The specification of these features for a Petri net can result in different classes of Petri nets. We consider each of these in turn.

6.3.1. Initial State

The initial state of a Petri net can be defined in several ways. The most common definition is to allow an arbitrary marking μ to be specified as an initial state. However, this definition can be modified in several ways. One convenient limitation is to restrict the initial state to a marking with one token in a start place and zero tokens elsewhere [Peterson 1976]. Another more general definition allows a set of initial markings rather than simply one marking.

These three definitions are essentially the same. Certainly the start place definition is a special case of the initial marking definition, which is a special case of the set of initial markings definition. However, if a set of initial markings M = { μ₁, μ₂, …, μ_k } is needed with a start place definition, we can simply augment the Petri net with an extra place p₀ and a set of transitions { t₁′, …, t_k′ } . Transition t_j′ would input a token from p₀ and would output marking μ_j. Thus the behavior of the augmented net would be identical to a Petri net with a set of initial markings, except that each transition sequence would be preceded with t_j′ if marking μ_j were used to start the execution.

We see then that these three definitions of start states for a Petri net are essentially equivalent. Out of a sense of tradition, we define a Petri net language as starting from a single arbitrary marking μ .

6.3.2. Labeling of Petri Nets

Labeling Petri nets is another situation where several definitions can be used. We must define both what the alphabet Σ of a Petri net should be and how it is to be associated with the Petri net. We have indicated that the symbols are associated with the transitions, so that a sequence of transition firings generates a string of symbols for the language. The association of symbols to transitions is made by a labeling function, σ: T → Σ . Variations in language definition may result from various restrictions placed on the labeling function.

A free-labeled Petri net is a labeled Petri net where all transitions are labeled distinctly [i.e., if σ ( t_i ) = σ ( t_j ), then t_i = t_j ]. The class of free Petri net languages is a subset of the class of Petri net languages with a more general labeling function which does not require distinct labels. An even more general labeling function has been considered which allows null labeled transitions, σ ( t_j ) = λ . These λ -labeled transitions do not appear in a sentence of a Petri net language, and their occurrence in an execution of a Petri net thus goes unrecorded. These three classes of labeling functions (free, λ -free, and with λ -transitions) define three variations of Petri net languages.

Without further investigation, it is not obvious which of these three labeling definitions is most reasonable. Perhaps each of the three is the most useful labeling function for some application. Thus, we need to consider the languages resulting from each possible definition of the labeling function.

6.3.3. Final States of a Petri Net

The definition of final states for a Petri net has a major effect upon the language of a Petri net. Four major different definitions of the final state set of a Petri net have been suggested. Each of these may produce different Petri net languages.

One definition is derived from the analogous concept for finite state machines. It defines the set of final states F as a finite set of final markings. For this definition we define the class of L-type Petri net languages.

DEFINITION 6.1

A language L is an L-type Petri net language if there exists a Petri net structure (P, T, I, O), a labeling of the transitions σ: T → Σ, an initial marking μ, and a finite set of final markings F such that L = { σ ( β ) ∈ Σ^* | β ∈ T^* and δ ( μ, β ) ∈ F } .

The class of L-type Petri net languages is rich and powerful, but it has been suggested that the requirement for a sentence to result in exactly a final state in order to be generated is contrary to the basic philosophy of a Petri net. This comment is based on the observation that if δ ( μ, t_j ) is defined for a marking μ and a transition t_j, then δ ( μ′, t_j ) is defined for any μ′ ≥ μ . From this comment we define a new class of languages, the class of G-type Petri net languages, by the following.

DEFINITION 6.2

A language L is a G-type Petri net language if there exists a Petri net structure (P, T, I, O), a labeling σ: T → Σ, an initial marking μ, and a finite set of final markings F, such that L = { σ ( β ) ∈ Σ^* | β ∈ T^* and there exists μ_f ∈ F such that δ ( μ, β ) ≥ μ_f } .

A third class of Petri net languages is the class of T-type Petri net languages. These are defined by identifying the set of final states used in the definition of L-type languages with the (not necessarily finite) set of terminal states. A state μ_t is terminal if σ ( μ_t, t_j ) is undefined for all t_j ∈ T. Thus the class of T-type Petri net languages is as follows.

DEFINITION 6.3

A language L is a T-type Petri net language if there exists a Petri net structure (P, T, I, O), a labeling σ: T → Σ, and an initial marking μ such that L = { σ ( β ) ∈ Σ^* | β ∈ T^* and δ ( μ, β ) is defined but for all t_j ∈ T, δ ( δ ( μ, β ), t_j ) is undefined } .

Still a fourth class of languages is the class of P-type Petri net languages whose final state set includes all reachable states. These languages are prefix languages since if α ∈ Σ^* is an element of a P-type language, then for all prefixes β of α ( α = β x for some x ∈ Σ^* ) β is an element of that same language.

DEFINITION 6.4

A language L is a P-type Petri net language if there exists a Petri net structure (P, T, I, O), a labeling σ: T → Σ, and an initial marking μ such that L = { σ ( β ) ∈ Σ^* | β ∈ T^* and δ ( μ, β ) is defined } .

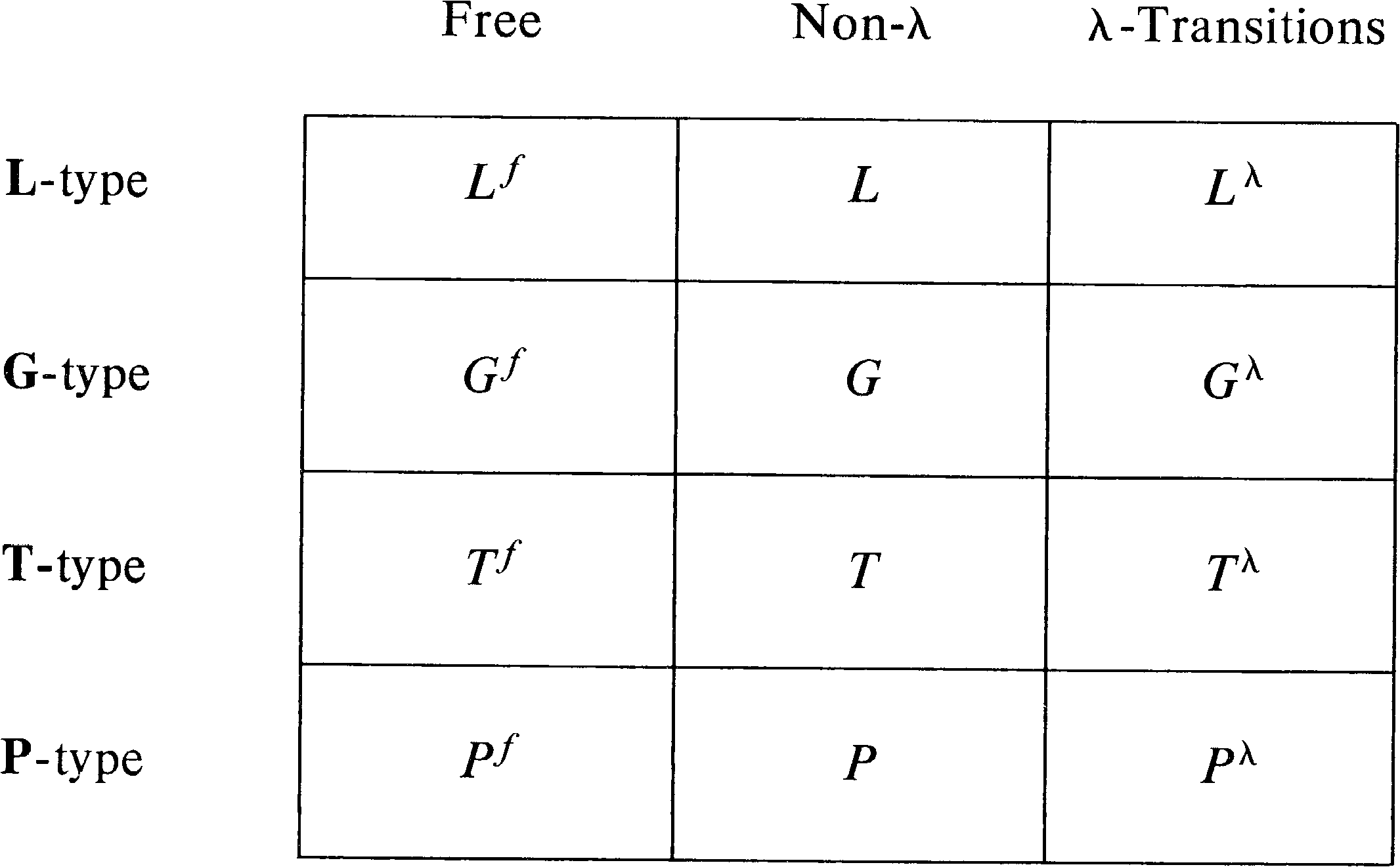
In addition to the four classes of languages based on different specifications of the final state set, we have the previously mentioned variations due to the labeling function. Figure 6.1 lists the 12 classes of languages which result from the cross product of the four types of final state specification and the three types of labeling functions. Each cell of Figure 6.1 lists the notation which is used to denote each class of Petri net language.

To specify a particular Petri net language, four quantities must be defined: the Petri net structure, C = (P, T, I, O) ; the labeling function, σ: T → Σ ; the initial marking, μ: P → N, and the set of final markings, F (for L- and G-type languages). We define γ = (C, σ, μ, F) to be a labeled Petri net with Petri net structure C, labeling σ, initial marking μ, and final state set F. For a given labeled Petri net γ, 12 languages can be defined: L ( γ ), G ( γ ), T ( γ ), P ( γ ), L^f ( γ ), G^f ( γ ), T^f ( γ ), P^f ( γ ), L^λ ( γ ), G^λ ( γ ), T^λ ( γ ), P^λ ( γ ) .

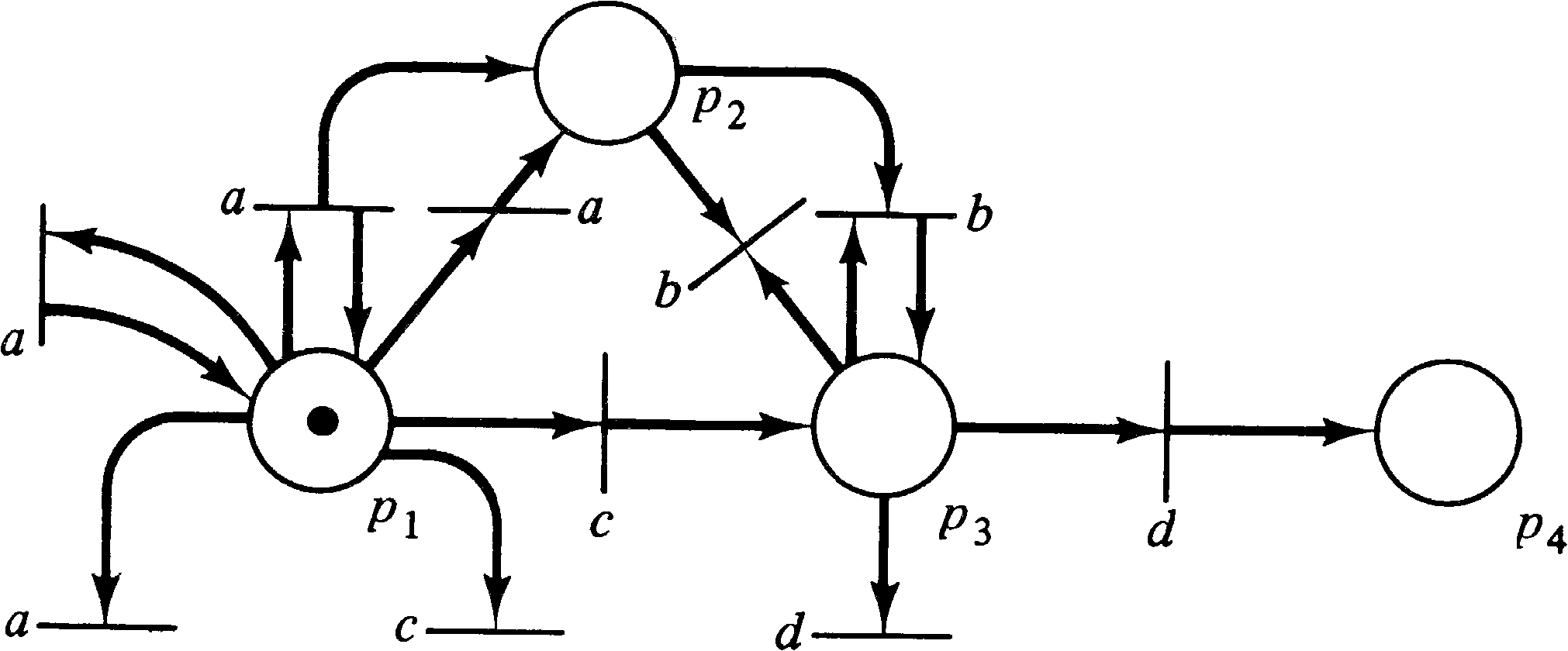
The different definitions of Petri net languages can associate different languages with a given Petri net. Consider, for example, the Petri net of Figure 6.2. The initial marking of (1, 0, 0, 0) is given on the net, and each transition t_j is labeled by σ ( t_j ) . If we define F = { (0, 0, 1, 0) } (one token in place p₃ ), the L-type language is { aⁿ c bⁿ | n ≥ 0 }, the G-type language is { a^m c bⁿ | m ≥ n ≥ 0 }, the T-type language is { a^m c bⁿ d | m ≥ n ≥ 0 }, and the P-type language is { a^m | m ≥ 0 } ∪ { a^m c bⁿ | m ≥ n ≥ 0 } ∪ { a^m c bⁿ d |m ≥ n ≥ 0 } . For this example, all four types of languages are different. The labeling function given is a free labeling, but by using different labeling functions, other languages can also be produced.

Despite the differences in definitions, the classes of Petri net languages are closely related. For instance, the set of free labelings is a subset of the set of non- λ labelings, which is a subset of the set of λ -labelings. Thus,

Also, every P-type language is a G-type language where F = { (0, 0, …, 0) } . Thus,

We can also show that each language of type G or G^λ is also a language of type L or L^λ, respectively. Let G be a G-type language for a Petri net structure (P, T, I, O), initial marking μ, and final set F. Construct a new labeled Petri net with the same places but with additional transitions as defined by the following:

For each t_j ∈ T, let B_j be the set of all proper subbags of O ( t_j ) . Each subbag in B_j is used to define a new transition with the same label and inputs as t_j but with the subbag as output. These new transitions are added to the previous set of transitions.

For example, if we consider the transition labeled a in the Petri net of Figure 6.2, its input bag is { p₁ }, and its output bag is { p₁, p₂ } . The subbags of { p₁, p₂ } are { p₁ }, { p₂ }, and { } ( = ∅ ). This transition would result in three new transitions being added to the net. All of these new transitions would be labeled a and have input bag { p₁ }, but the output bags would be the three subbags listed above (one transition for each subbag). New transitions would also be added for the transitions labeled b, c, and d, which would have the same inputs but null outputs (since the current outputs are singleton bags and hence the only subbag is ∅ ). This new net is shown in Figure 6.3.

This new net has been modified in such a way that the “extra” tokens which exceed a final state in F need not be produced, if one selects the appropriate new transition which has fewer outputs. Thus the L-type language of the new net is the same as the G-type language of the old net.

The above construction can also be modified slightly to show that a generalization of the definition of L-type languages (to permit incompletely specified final markings) does not change the classes L and L^λ. Let a final marking for a Petri net with n places be an n -vector over N ∪ { ω } . If a component of a final marking is ω, this means we do not care what the value of that component is in a final state. A state s is a final state if there exists a final marking f such that for all i, 1 ≤ i ≤ n, if f_i ≠ ω, then s_i = f_i. This is obviously a more general definition than the definition of L-type languages given earlier.

Now consider a language which is defined by a Petri net and an incompletely specified final marking, f. Let τ be the set of all places for which f_i = ω . For each transition t_j ∈ T for which O ( t_j ) ∩ τ ≠ ∅, let ρ_j = O ( t_j ) ∩ τ and ψ_j = O ( t_j ) − ρ_j. The bag ρ_j is all places whose markings are don't-cares, while the bag ψ_j is all places whose markings must be exactly as specified in the final marking f. We add new transitions to the net whose label and input bag are the same as the label and input bag for t_j but whose output bag is ψ_j + ξ, where ξ ranges over all subbags of ρ_j. This construction does not in any way modify the behavior of those places which are not in τ but allows those places which are don't-cares to have any number of tokens less than or equal to the number of tokens which would have appeared in the original net. Thus, for each sentence in the generalized language of the original net, it is possible to pick appropriate transitions to fire so that when the net reaches a state s such that s_i = f_i for f_i ≠ ω, then s_i = 0 for f_i = ω . Thus the L-type language for the constructed Petri net with a final marking f′ (where all ω in the incompletely specified marking f have been replaced by 0) is the same as the generalized language of the original net (as defined by the incompletely specified final marking f ).

For a language defined by a set of incompletely specified final markings (as opposed to only one such marking as just discussed), we use the fact that L (and L^λ ) languages are closed under union (see Section 6.5.2) to show that the language is still an L (or L^λ ) language.

With the introduction of incompletely specified final markings, we can show that T-type languages are also L-type languages (except possibly for free T-type languages).

A final state μ for a T-type language is such that no transition t_j can fire [i.e., ≥ μ ≱ I ( t_j )">] for all t_j ∈ T ]. The condition which specifies a final state for a T-type language is thus exactly the opposite of the condition specifying a final state for a G-type language. (We might call the T-type languages inverse G-type languages.) It is not difficult to see that such a set of markings can be described by a finite set of incompletely specified markings (as was done in Section 5.4). For example, the condition [≥ μ ≱ (2, 0) and ≥ μ ≱ (1, 1) ] is equivalent to [ μ = (0, ω ) or μ = (1, 0) ]. A T-type language (or, more generally, an inverse G-type language) can thus be rewritten as a generalized (i.e., incompletely specified) L-type language and then as an L-type language. Thus T ⊆ L, and T^λ ⊆ L^λ.

It is known that every L^λ -type language can be generated by a Petri net in which every transition has an input place, and where the unique final marking is the zero marking, at which no transition is fireable [Hack 1975b]. If we add to every place a λ -transition with a single input and a single output of that same place (i.e., a self-loop), then the language is not changed, and the zero marking becomes the only terminal marking. Hence, L^λ ⊆ T^λ, and from our previous demonstration that T^λ ⊆ L^λ, these two classes of languages are identical, T^λ = L^λ.

Figure 6.4 represents graphically the relationships among the classes of Petri net languages which we have just derived. An arc between classes indicates the containment of one class of Petri net languages within another.

The study of Petri net languages is just beginning, and at present knowledge of the properties of these newly defined classes of languages is limited. The power of Petri nets is reflected in the variety of potentially different classes of Petri net languages which can be defined. The newness of this research is reflected by our inability to either show the complete relationships between these languages, or to argue that only a few of these classes are of importance. This results in a vast field of study, with the need to develop the properties of 12 different classes of languages.

It is obviously not possible to develop all 12 classes of languages in this volume, and so we limit ourselves here to considering only one class of Petri net languages, the L-type languages. The major reasons for this limitation are space and the fact that this language has been investigated in the literature [Peterson 1973; Hack 1975b; Peterson 1976]. Some results have also been obtained by Hack [1975b] for the prefix (P-type) languages and will be presented in our summary. The G-type and T-type languages have been defined, but no work has been done on their development. Remember also that the class of L-type languages includes the classes of T-type, G-type, and P-type languages. Thus, L-type languages are in some sense the largest class of Petri net languages and so are appropriately investigated first.

Our investigation of the properties of L-type Petri net languages will focus on two aspects. First we present closure properties of Petri nets under certain common operations (concatenation, union, concurrency, intersection, reversal, complement, indefinite concatenation, and substitution). Then we consider the relationship between Petri net languages and the classical formal languages: regular, context-free, context-sensitive, and type-0. This presentation provides an understanding of the power and limitations of (L-type) Petri net languages. It also indicates how the other classes of Petri net languages can be investigated.

Although we are interested in the entire class of L-type Petri net languages, we limit our discussion to only a limited set of standard form Petri nets. This limitation is made in order to ease the proofs and constructions; it does not limit the class of Petri net languages. For every Petri net language, there may be many Petri nets which generate that language; we choose to work only with those nets with certain properties. To show that this does not reduce the set of languages, we show that for every L-type Petri net language there exists a standard form Petri net which generates it.

First we define a standard form Petri net.

DEFINITION 6.5

A labeled Petri net γ = (C, σ, μ, F) with language L ( γ ) in standard form satisfies the following properties:

1. The initial marking μ consists of exactly one token in a start place p_s and zero tokens elsewhere. p_s ∉ O ( t_j ) for all t_j ∈ T.

2. There exists a place p_f ∈ P such that

   1. F = { p_f } [if λ ∉ L ( γ ) ] or F = { p_f, p_s } [if λ ∈ L ( γ ) ].

   2. p_f ∉ I ( t_j ) for all t_j ∈ T.

   3. δ ( μ′, t_j ) is undefined for all t_j ∈ T, and μ′ ∈ R ( C, μ ) which have a token in p_f [i.e., μ′ ( p_f ) > 0 ].

The execution of a Petri net in standard form begins with one token in the start place. The first transition which fires removes this token from the start place, and after this firing the start place is always empty. Eventually the Petri net may stop by placing one token in the final place. This token cannot be removed from the final place both because no place has an input from the final place and because all transitions are disabled. Thus the execution of a Petri net in standard form is quite simple and limited. This is of great use when compositions of Petri nets are constructed. To show that Petri nets in standard form are not less powerful than general Petri nets, we prove the following theorem.

THEOREM 6.1

Every Petri net is equivalent to a Petri net in standard form.

Proof :

The proof is by construction. Let γ = (C, σ, μ, F) be a labeled Petri net with C = (P, T, I, O) . We show how to construct an equivalent γ′ = (C′, σ′, μ′, F′ ) with C′ = (P′, T′, I′, O′ ) which is in standard form (Figure 6.5).

---

Figure 6.5. The constructed form of a Petri net in standard form. The execution of the net is the same as the original net, but the new net is in standard form.

---

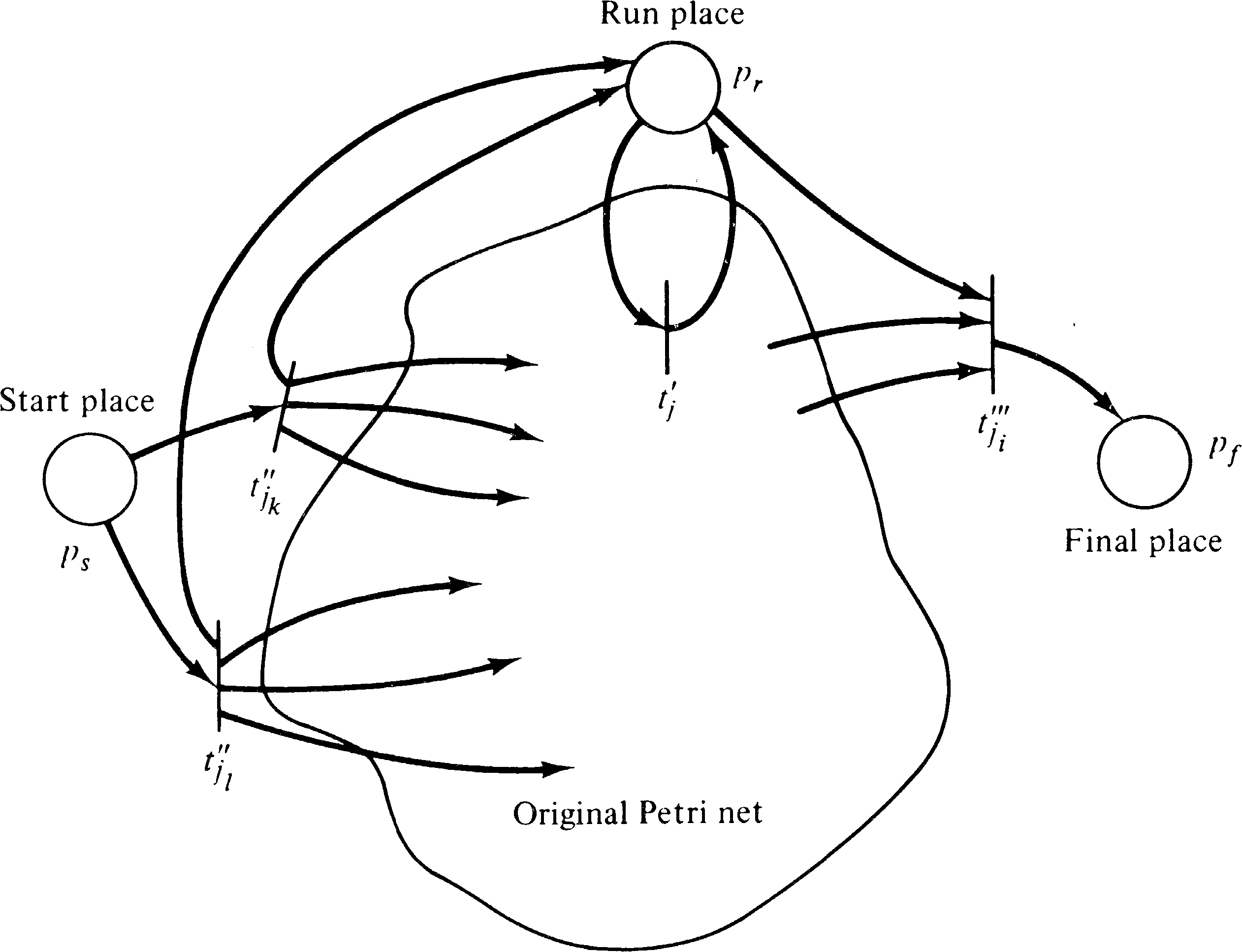
To start, we define three new places p_r, p_f, and p_s which are not in p. Place p_s is the start place, place p_f is the final place, and p_r is a “run” place; a token must be in p_r to allow any transition in T to fire. The initial marking of C′ will have one token in p_s; the final marking will consist of one token in p_s [if λ ∈ L ( γ ) ] or p_f [for λ ∉ L ( γ ) ].

Now we wish to be sure that every transition sequence in C leading from the initial marking to a final marking is “mimicked” in C′ . To this end we consider three types of strings in L ( γ ) . First, the empty string λ is properly handled by the definition of F′ . We can determine if λ ∈ L ( γ ) by checking if the initial marking μ is a final marking μ ∈ F. Second, for all strings of length 1 in L ( γ ), we include a special transition from p_s to p_f in C′ as follows: For α ∈ Σ with α ∈ L ( γ ), define t_α ∈ T′, with I ( t_α ) = { p_s } and O ( t_α ) = { p_f } . The label for t_α is α . We can determine if α ∈ L ( γ ) by checking all transitions t_j ∈ T, with σ ( t_j ) = α, to see if δ ( μ, t_j ) ∈ F.

Finally, consider all strings of length greater than 1. These strings result from a transition sequence

tj1 tj2... tji

of transitions in T. We would like to define a sequence

a tj1′ ⋯ tji′ b

with new transitions a and b. The new transition a would input a token from p_s and output the initial marking μ of C plus a token in p_r. Every transition t_j′ in T′ is the same as t_j in T except that p_r is an input and an output. This allows us to disable all transitions in T′ -- by removing the token in p_r. Finally, the transition b would remove the token from p_r and a final marking of C and output a token to p_f. With this construction, the token in the start place would move to the final place in C′ only as a result of a sequence

a tj1′ ⋯ tji′ b

which corresponds to a sequence

tj1... tji

leading from μ to a final marking in C.

Unfortunately this would produce a sequence which is too long since the extra symbols corresponding to transitions a and b would exist for C′ but not for C. One solution would be a null labeling for a and b, but the L-type languages do not allow null labelings. So to solve this problem we are forced to collapse transitions a and t_j1′ into one transition t_j1′′ and collapse transition b and t_ji′ into t_ji′′′ . Thus for all t_j ∈ T we define the following transitions in T′:

1. Define t_j′ ∈ T′, with I ( t_j′ ) = I ( t_j ) ∪ { p_r } and O ( t_j′ ) = O ( t_j ) ∪ { p_r } .

2. If I ( t_j ) ⊆ μ (i.e., the inputs to t_j are a subset of the initial marking, so that t_j could be the first transition to fire), define a transition t_j′′ with I ( t_j′′ ) = { p_s } and O ( t_j′′ ) = μ − I ( t_j ) + O ( t_j ) ∪ { p_r } .

3. If O ( t_j ) ⊆ μ′ for some μ′ ∈ F"> (so that t_j could be the final transition which fires, leading to a final marking), define a transition t_j′′′ with I ( t_j′′′ ) = μ′ − O ( t_j ) + I ( t_j ) ∪ { p_r } and O ( t_j′′′ ) = { p_f } .

Now we define the labeling σ′ by

σ′(tj′)

=

σ′(tj′′)

=

σ′(tj′′′)

=

σ(tj)

Any string α ∈ L ( γ ) is by definition generated by a sequence t_j1 t_j2... t_ji with α = σ ( t_j1 t_j2... t_ji ) . By construction

α

=

σ′(tj1′′ tj2′ ⋯ tji − 1′ tji′′′)

and so α ∈ L ( γ ) . Thus, since L ( γ ) = L ( γ′ ), the two nets γ and γ′ are equivalent. By construction γ′ is in standard form. Q.E.D.

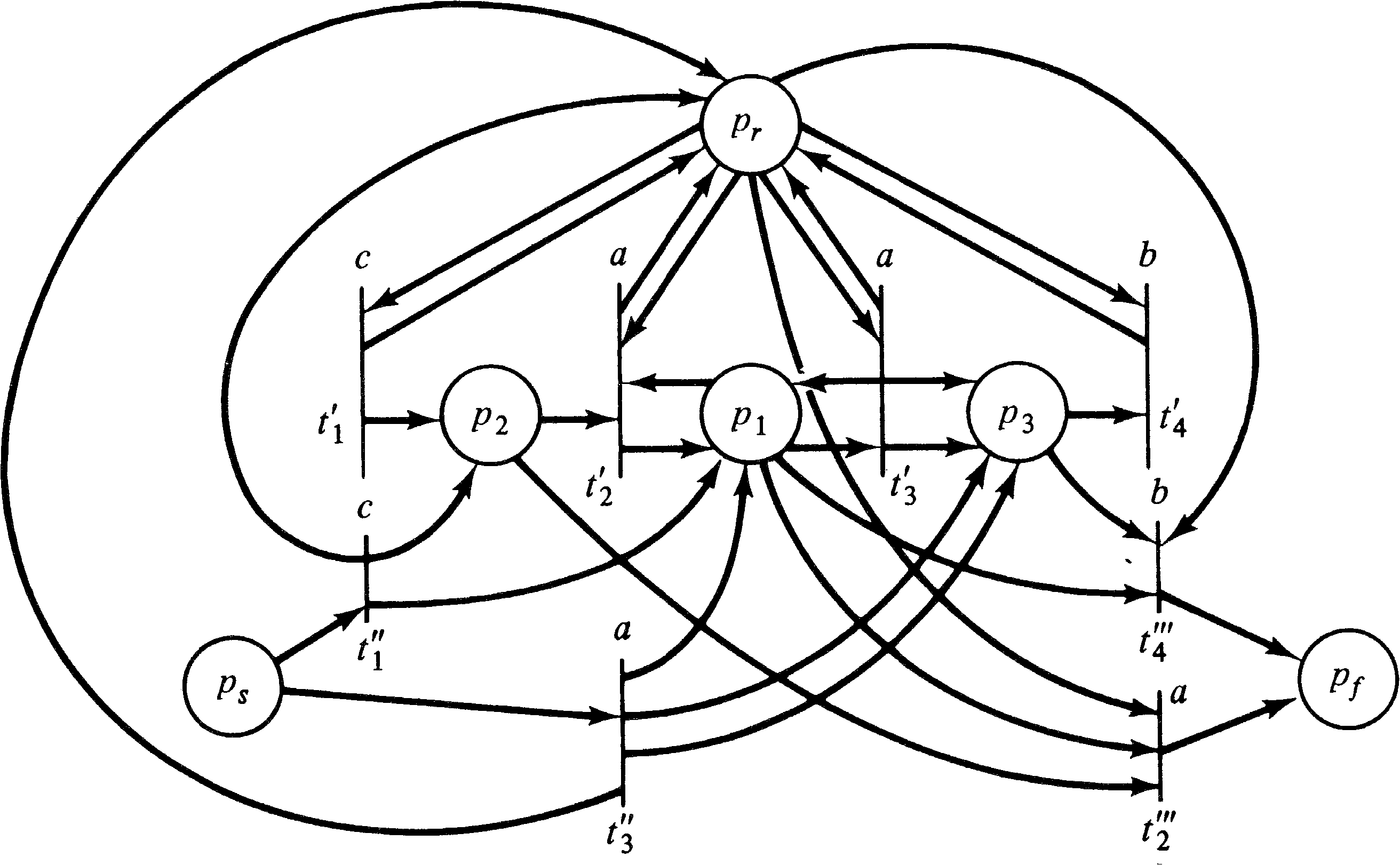
Figure 6.6 gives a simple Petri net which is not in standard form. Applying the construction of the proof to this Petri net produces the standard form Petri net of Figure 6.7.

We now examine the closure properties of Petri net languages under several forms of composition (union, intersection, concatenation, concurrency, and substitution) and under some operations (reversal, complement, and indefinite concatenation). The motivation for this examination is twofold. First, it increases our understanding of the properties and limits of Petri net languages as languages. Second, many of these compositions reflect how large systems are designed and constructed by the composition of smaller systems into larger systems. Thus, this investigation may help in the development of synthesis techniques.

Most of the closure properties deal with compositions of Petri net languages. For this we assume two Petri net languages L₁ and L₂. We know that each of these languages is generated by some Petri net in standard form. Thus, we consider the two standard form labeled Petri nets γ₁ = (C₁, σ₁, μ₁, F₁ ) and γ₂ = (C₂, σ₂, μ₂, F₂ ) with L₁ = L ( γ₁ ) and L₂ = L ( γ₂ ) . Since they are in standard form, γ₁ has a start place p_s1 ∈ P₁ and γ₂ has p_s2 ∈ P₂. Also F₁ = { p_s1, p_f1 } or { p_f1 } and F₂ = { p_s2, p_f2 } or { p_f2 } .

From these two labeled Petri nets we show how to construct a new labeled Petri net γ′ = (C′, σ′, μ′, F′ ) with language L ( γ′ ) which is the desired composition of L₁ and L₂. We illustrate these constructions with example Petri nets.

We begin by considering the composition of two Petri net languages by concatenation, union, intersection, and concurrency. Then we consider the reversal and complement of a Petri net language and, finally, substitution.

6.5.1. Concatenation

Many systems are composed of two sequential subsystems. Each of the subsystems may separately be expressed as a Petri net with its own Petri net language. When the two systems are combined sequentially, the resulting execution is the concatenation of an execution from the first Petri net language with an execution from the second. The concatenation of two languages can be formally expressed as

THEOREM 6.2

If L₁ and L₂ are Petri net languages, then L₁L₂ is a Petri net language.

Proof :

Define γ′ such that the final place of γ₁ overlaps with the start place of γ₂. Then the transition which places a token in p_f1, signaling an end to the execution of γ₁, also signals the start of an execution of γ₂. Any string in the concatenation of L₁ and L₂ thus has a path from p_s1 to p_f1 = p_s2 and then to p_f2 in the composite Petri net and is an element of L ( γ′ ) . Similarly, if a string is generated by C′, it must be composed of a string generated by γ₁, followed by a string in γ₂.

The formal definition of γ′ must take into consideration the empty string and so is more complex but can be defined as the union of γ₁ and γ₂ with the following extra transitions. For each transition t_j ∈ T₂ with I₂( t_j ) = { p_s2 }, we introduce a new transition t_j′ with I′ ( t_j′ ) = { p_f1 } and O′ ( t_j′ ) = O₂( t_j ) . If p_s1 ∈ F₁, then we also add t_j′′ with I′ ( t_j′′ ) = { p_s1 } and O′ ( t_j′′ ) = O₂( t_j ) . We define σ′ ( t_j′ ) = σ₂( t_j ) and σ′ ( t_j′′ ) = σ₂( t_j ) . The new final set F′ is F₁ ∪ F₂ if p_s2 ∈ F₂; otherwise F′ = F₂. Q.E.D.

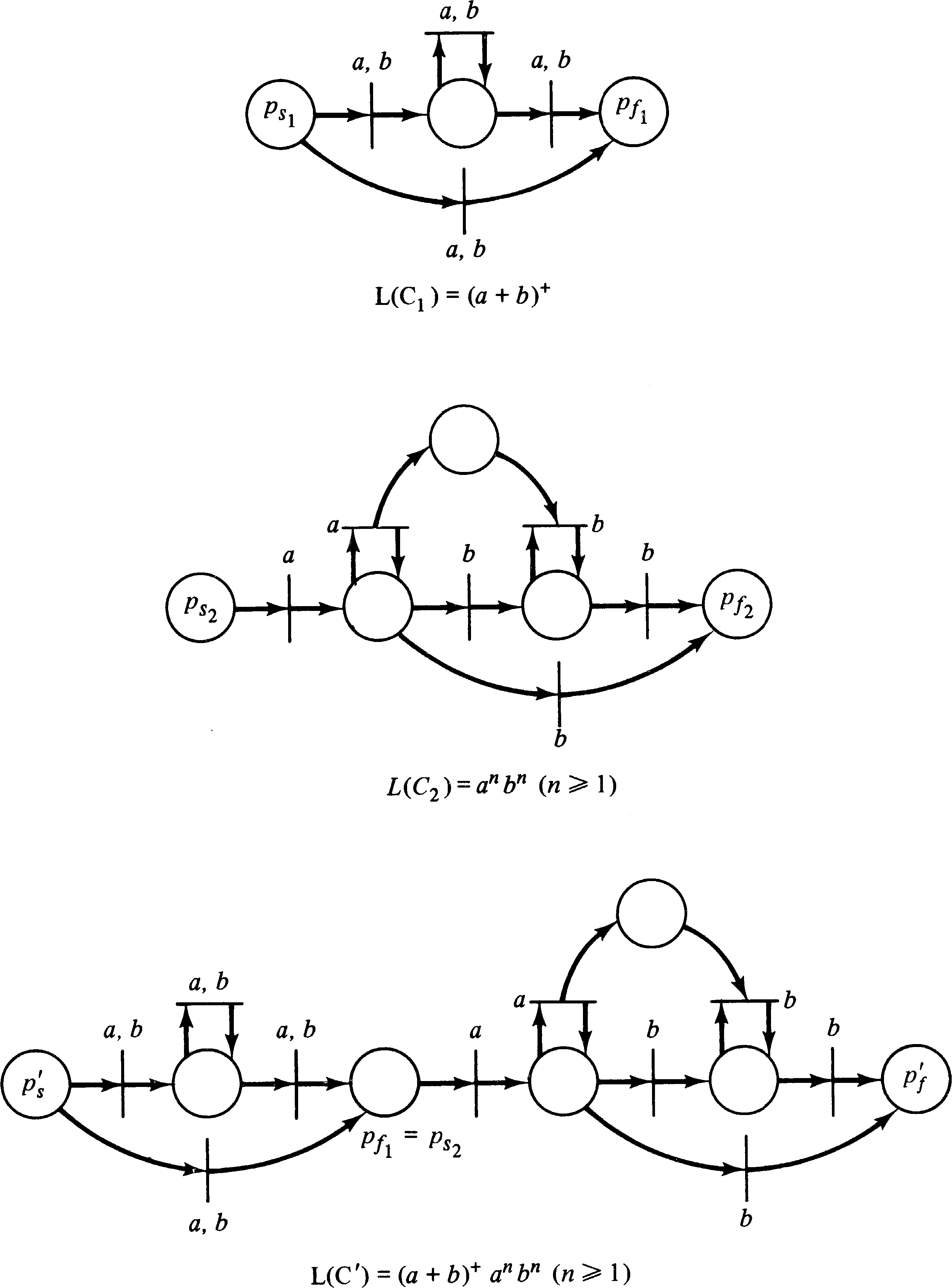
This shows that Petri net languages are closed under concatenation. Figure 6.8 illustrates this construction for L₁ = ( a + b )⁺ and L₂ = aⁿ bⁿ.

Another common method of combining systems is union. In this composition either one, but only one, of the subsystems will be executed. This is similar to set union and is a common composition of languages. It can be defined by

THEOREM 6.3

If L₁ and L₂ are Petri net languages, then L₁ ∪ L₂ is a Petri net language.

Proof :

The proof of this theorem is similar to the proof of the previous theorem. We define a new Petri net γ′ such that L ( γ′ ) = L₁ ∪ L₂. The new Petri net combines the two start places into one new start place. Then the first transition which fires removes the token from the start place, and either the Petri net γ₁ (if the transition was in T₁ ) or the Petri net γ₂ (if the transition was in T₂ ) continues to operate exactly as it had before.

Formally we define a new start place p_s′ and new transitions t_j1′ for each t_j1 ∈ T₁ with I ( t_j1 ) = p_s1 and t_j2′ for each t_j2 ∈ T₂ with I ( t_j2 ) = p_s2. We define I′ ( t_j1′ ) = p_s′ and I′ ( t_j2′ ) = p_s′ with O′ ( t_j1′ ) = O₁( t_j1 ) and O′ ( t_j2′ ) = O₂( t_j2 ) . The labeling function σ′ ( t_j1′ ) = σ₁( t_j1 ) and σ′ ( t_j2 ) = σ₂( t_j2 ) . The new initial marking has one token in p_s′ ; the new final marking set F′ = F₁ ∪ F₂. If p_s1 ∈ F₁ or p_s1 ∈ F₂, then p_s′ ∈ F′ also. Q.E.D.

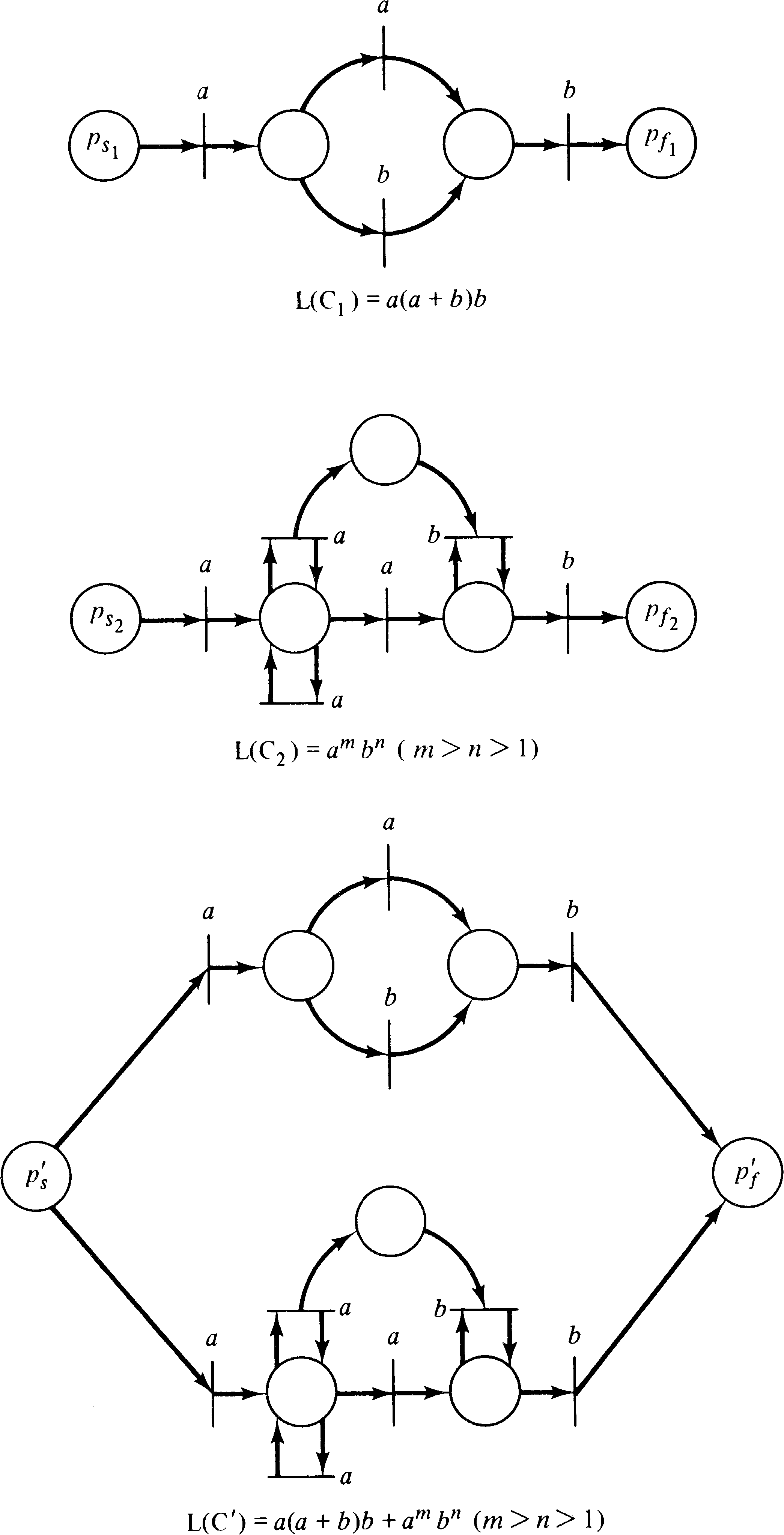
Still another way of combining two Petri nets is by allowing the executions of two systems to occur concurrently. This allows all possible interleavings of an execution of one Petri net with an execution of the other Petri net. Riddle [1972] has introduced the || operator to represent this concurrency. It can be defined for a, b ∈ Σ and x₁, x₂ ∈ Σ^* by

It is easily shown that regular, context-sensitive, and type-0 languages are closed under concurrency by demonstrating that the cross product of two finite state machines, linear bounded automata, or Turing machines is still a finite state machine, linear bounded automaton, or Turing machine, respectively. Since the cross product of two pushdown stack automata cannot be transformed into another pushdown stack automaton, context-free languages are not closed under concurrency. For Petri net languages, we have the following theorem.

THEOREM 6.4

If L₁ and L₂ are Petri net languages, then L₁ || L₂ is a Petri net language.

Proof :

The construction of a Petri net to generate the concurrent composition of L₁ and L₂, given Petri nets generating these Petri net languages, is basically a Petri net which places tokens in the start places of both γ₁ and γ₂, as an initial marking, and defines the new final marking set to be any marking which is in F₁ (over the places of P₁ ) and is in F₂ (over the places of P₂ ). Q.E.D.

This construction is illustrated in Figure 6.10 for L₁ = a ( a + b )⁺ and L₂ = c a³ⁿ c b²ⁿ c.

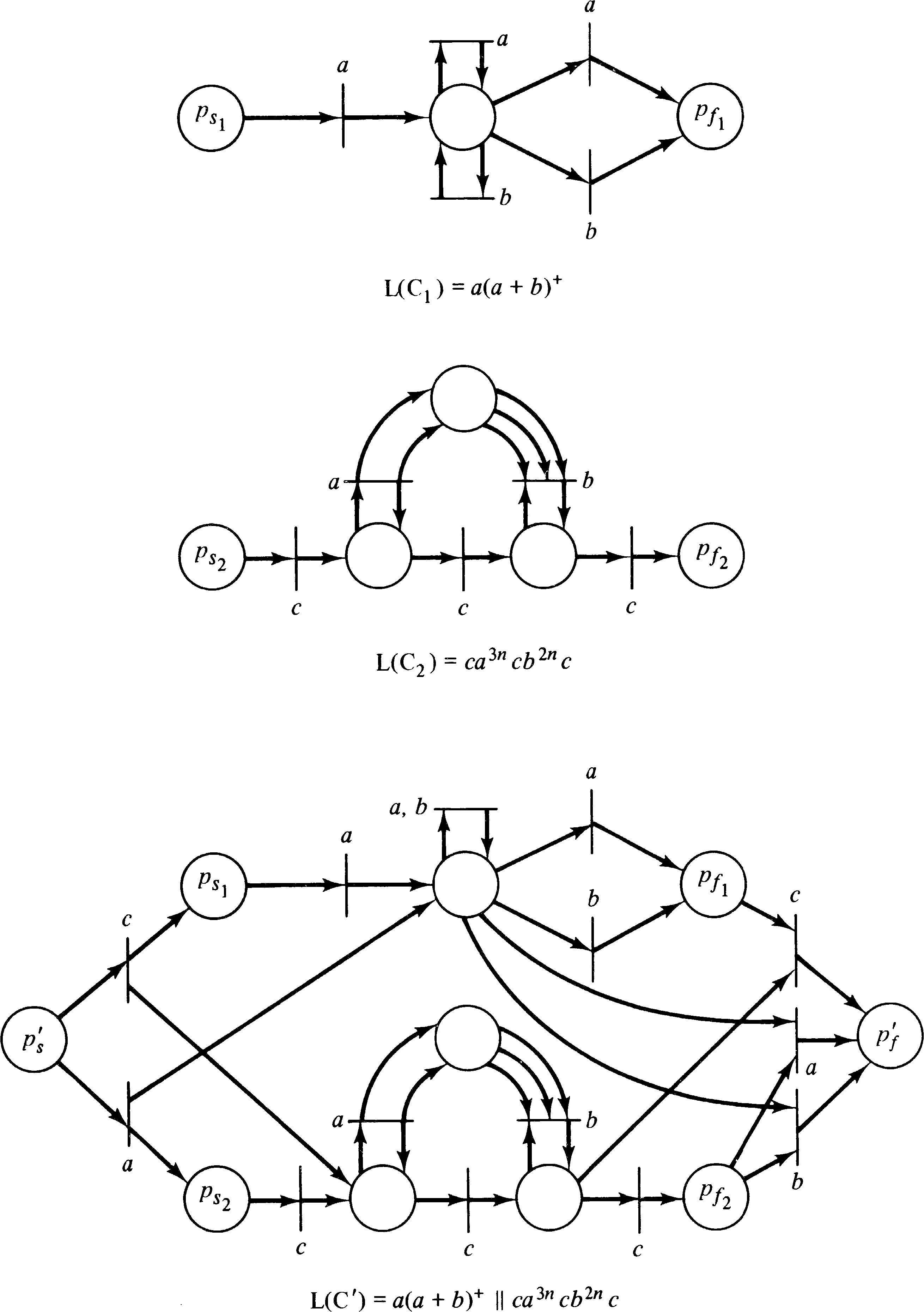
As with union, the intersection composition is similar to the set theory definition of intersection and is given for a Petri net language by

THEOREM 6.5

If L₁ and L₂ are Petri net languages, then L₁ ∩ L₂ is a Petri net language.

The construction of a Petri net to generate the intersection of two Petri net languages is rather complex. At a given point in the generated string, if a transition fires in one Petri net, there must be a transition in the other Petri net with the same label which fires also. When more than one transition exists in each Petri net with the same label, we must consider all possible pairs of transitions from the two Petri nets. For each of these pairs, we create a new transition which fires if and only if both transitions fire in the old Petri nets. This is done by making the input (output) bag of the new transition the bag sum (see the appendix) of the input (output) bags of the pair of transitions from the old Petri nets. Thus if t_j ∈ T₁ and t_k ∈ T₂ are such that σ ( t_j ) = σ ( t_k ), then we have a transition t_{j, k} ∈ T′ with I′ ( t_{j, k} ) = I₁( t_j ) + I₂( t_k ) and O′ ( t_{j, k} ) = O₁( t_j ) + O₂( t_k ) . Some of these transitions have inputs which include the start place. If for a transition t_{j, k} in T′, as defined above, I′ ( t_{j, k} ) = { p_s1, p_s2 }, then we replace this transition with a new transition t_{j, k}′, where I′ ( t_{j, k}′ ) = { p_s′ } . This construction essentially places the two original Petri nets in a lockstep identical execution mode. This composite Petri net generates the intersection of L₁ and L₂. The construction is demonstrated in Figure 6.11.

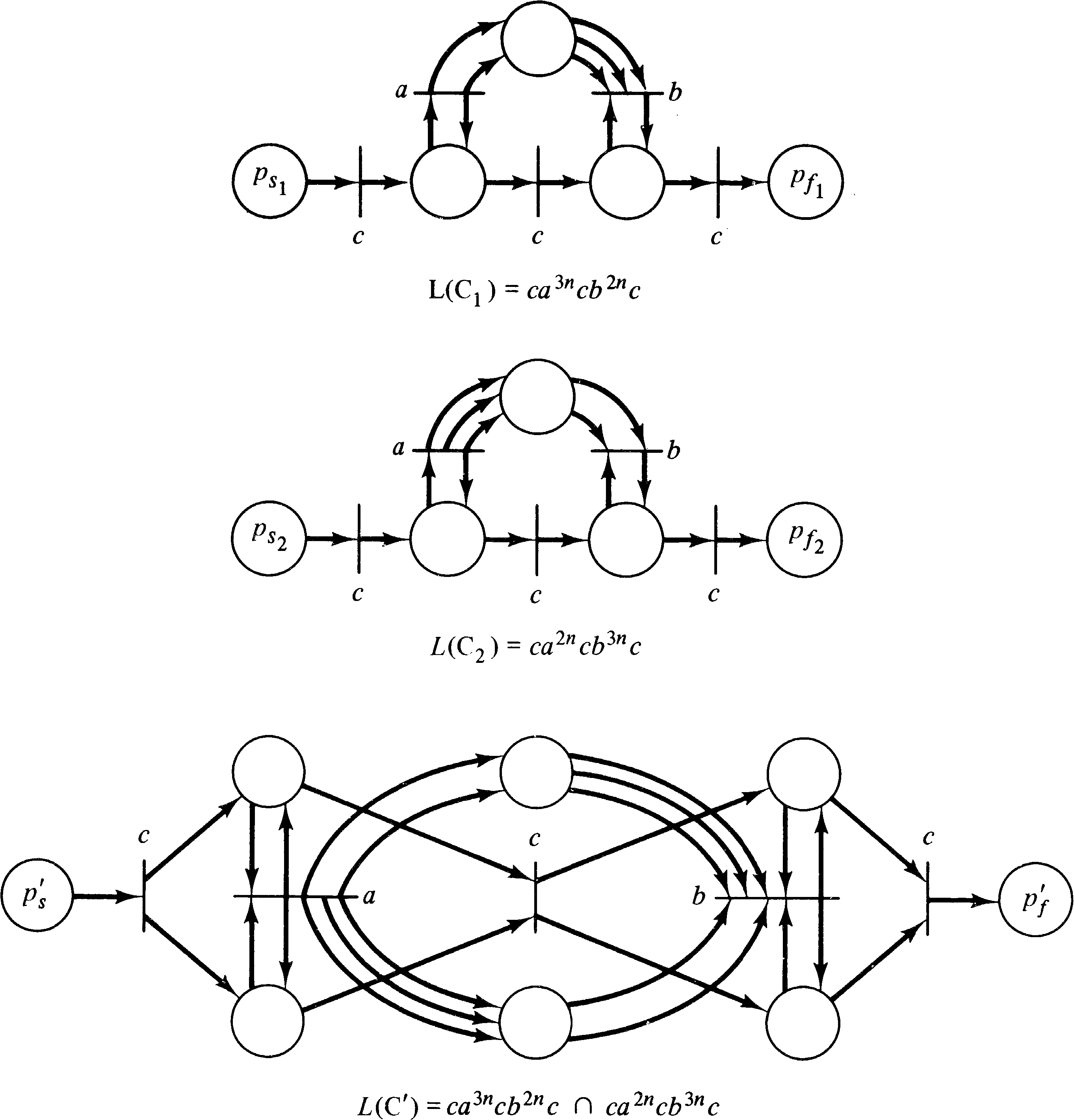
Unlike the previous composition operations which we have examined, the operation of reversal seems to have only academic interest. The reversal of a sentence x^R is the sentence x with its symbols in the reverse order. We define this recursively by

THEOREM 6.6

If L is a Petri net language, then L^R is a Petri net language.

The construction is trivial. The start and final markings are interchanged, and the input and output bags for each transition are also interchanged and L ( γ′ ) = L ( γ )^R. This merely runs the Petri net backwards and reverses all generated strings.

6.5.6. Complement

The complement L of a language L over an alphabet Σ is the set of all strings in Σ^* which are not in L. This can be expressed as

Closure under complement for the L-type Petri net languages is an open problem. However, Crespi-Reghizzi and Mandrioli [1977] have shown that some Petri net languages are not closed under complement; that is, there are Petri net languages whose complement is not a Petri net language.

6.5.7. Repeated Composition

So far we have considered the operations of union, intersection, concatenation, concurrency, reversal, and complement. Except for the last operation, we were able to give constructions that show that Petri net languages are closed under these operations. From these results we can immediately derive the following corollary.

COROLLARY 6.1

Petri net languages are closed under any finite number of applications, in any order, of the operations of union, intersection, reversal, concurrency, and concatenation.

A new operation can be defined by removing the constraint that only a finite number of compositions be allowed. The indefinite concatenation (Kleene star) of a language is the set of all concatenations (of any length) of elements from that language. This is represented by L^* and is defined by

This operation may be of practical use. Indefinite concatenation is similar to the modeling of a loop. Also it is known that regular, context-free, context-sensitive, and type-0 languages are closed under indefinite concatenation [Hopcroft and Ullman 1969]. Thus it is unexpected and perhaps unfortunate that Petri net languages are not closed under indefinite concatenation.

This appears to be due to the combination of the finite nature of Petri nets (finite number of places and transitions) and the permissive nature of the state changes [transitions are allowed (permitted) to fire but cannot be required to do so]. To construct a Petri net to generate the indefinite concatenation of a Petri net language would, in general, require the reuse of some portion of the Petri net. This allows tokens to be generated and left in some of the places which are reused. At a later repetition of the Petri net, these tokens may be used to allow transitions to fire when they should not.

The proof that Petri nets are not closed under indefinite concatenation appears to be very difficult. Perhaps a flavor of the approach can be given by considering an example. We have already seen that aⁿ bⁿ ( n > 1 ) is a Petri net language. We claim that ( aⁿ bⁿ )^* is not a Petri net language. All generators of ( aⁿ bⁿ )^* must have some place or set of places that encode the number n for each portion of the string. These tokens control the generation of the b symbols. For a Petri net to generate ( aⁿ bⁿ )^* it is necessary to use these places more than once. But since the net is permissive, there is no way to guarantee that these places are empty before they are reused. Thus for any Petri net which attempts to generate ( aⁿ bⁿ )^* there exists some i, j, k such that the Petri net also generates some string of the following form:

For readers familiar with the formal language theory of Abstract Families of Languages (AFL) [Ginsburg 1975], it is easy to prove that Petri net languages are not closed under indefinite concatenation. It is well known that the smallest full AFL closed under intersection and containing { aⁿ bⁿ } contains every recursively enumerable set. Thus, since Petri net languages are closed under intersection and { aⁿ bⁿ } is a Petri net language, if they were closed under indefinite concatenation, they would be such an AFL. However, we know that { w w^R } is not a Petri net language (see Section 6.6.2), and so Petri net languages are not closed under indefinite concatenation. This argument is due to Mandrioli.

A subclass of Petri net languages exists which is closed under indefinite concatenation, however. This is the class of Petri net languages for properly terminating Petri nets. Proper termination was defined by Gostelow [1971] for complex bilogic graph models of computation. We borrow his definition and rephrase it in terms of Petri nets as follows.

DEFINITION 6.6

A Petri net is properly terminating if whenever it terminates it is guaranteed that (1) only one token remains in the Petri net and it is in the final place and (2) the number of tokens used in the Petri net is finite.

We notice first that the second part of the definition is not actually a restriction since if the Petri net terminates, then it terminates in a finite amount of time and hence generates only a finite number of tokens. But the first part of the definition is a restriction. We may view the Petri net as a machine which generates strings of symbols. We place a token in the input to the machine, and a string of symbols is printed on a piece of tape for us. Eventually a light may come on saying that the machine has halted (i.e., there are no enabled transitions). In normal use, before we can use the printed output, we must look inside the machine and check that a final marking has been reached. If a final marking has not been reached, then we must reject the output and try again. If the Petri net is properly terminating, then we need not look inside the machine; we are guaranteed that a final marking has been reached.

We can see then how a properly terminating Petri net can be used to construct a Petri net generating the indefinite concatenation of its language. We simply connect the final place to the start place. Since the Petri net is known to be empty whenever a token appears at the final place, no tokens will be left in the Petri net to cause spurious transitions when the Petri net is reused.

Unfortunately, this subclass of Petri nets is not very interesting since we can show that all properly terminating Petri nets are finite state machines and vice versa. Hence the Petri net languages of properly terminating Petri nets are regular languages, and it is already known that this class of languages is closed under indefinite concatenation. Thus we see that the properties of systems modeled by Petri net languages are limited to finite repetitions of smaller subsystems or indefinite repetitions of smaller finite subsystems.

6.5.8. Substitution

We have mentioned that systems can be designed and modeled hierarchically by Petri nets. This involves first specifying a rough outline of the system and then successively refining this outline by substituting for operations the definitions of these operations in terms of other operations. With Petri nets, this refinement may take the form of substituting a complete Petri net for a transition or a place. The latter is very straightforward; we therefore restrict our attention to considering the problem of substituting a subnet for a transition (or operation) of a Petri net.

When it is desired to substitute a Petri net for an operation in another Petri net, this can be considered as a composition of the Petri net languages of the two Petri nets. Since the operation is represented by a symbol from Σ, substitution of a Petri net language L₂ for a symbol σ in another Petri net language L₁ is defined as the replacement of all occurrences of σ in L₁ by the set of strings L₂. Petri net languages are closed under substitution if the result of a substitution involving a Petri net language is also a Petri net language. Variations on substitution include finite substitution, where L₂ must be a finite set of strings, and homomorphism, where L₂ is a single string.

Again, unfortunately, we have a negative result. Petri net languages are not closed under general substitution. This is shown immediately by letting L₁ = c^* and substituting L₂ = aⁿ bⁿ for c in L₁. The problem is again caused by the possible reuse of a Petri net. For finite substitution and homomorphism, however, we see that L₂ is a regular language, and hence a properly terminating Petri net can be constructed to generate it. This yields the following theorem and corollary.

THEOREM 6.7

If L₂ is a regular language and L₁ is a Petri net language, then the result of substituting L₂ for a symbol in L₁ is a Petri net language.

COROLLARY 6.2

Petri net languages are closed under finite substitution and homomorphism.

Having considered the properties of Petri net languages as a class of languages, we turn to investigating the relationship between Petri net languages and other classes of languages. In particular, we consider the classes of regular, context-free, context-sensitive, and type-0 languages.

6.6.1. Regular Languages

One of the simplest and most studied classes of formal languages is the class of regular languages. These languages are generated by regular grammars and finite state machines. They are characterized by regular expressions. Problems of equivalence or inclusion between two regular languages are decidable, and algorithms exist for their solution [Hopcroft and Ullman 1969]. With such a desirable set of properties, it is encouraging that we have the following theorem.

THEOREM 6.8

Every regular language is a Petri net language.

The proof of this theorem is based on the fact that every regular language is generated by some finite state machine and we have shown (Section 3.3.1) that every finite state machine can be converted to an equivalent Petri net.

The converse to this theorem is not true. Figure 6.12 displays a Petri net which generates the context-free language { aⁿ bⁿ | n > 1 } . Since this language is not regular, we know that not all Petri net languages are regular languages.

Figure 6.12 demonstrated that not all Petri net languages are regular languages by exhibiting a Petri net language which was context-free but not regular. Figure 6.13 shows that not all Petri net languages are context-free by exhibiting a Petri net language which is context-sensitive but not context-free. Unlike the situation with regular languages, however, there also exist context-free languages that are not Petri net languages. An example of such a language is the context-free language { w w^R | w ∈ Σ^* } . This results in the following theorem.

THEOREM 6.9

There exist context-free languages which are not Petri net languages.

Proof :

Assume there exists an n -place, m -transition Petri net which generates the language w w^R. Let k be the number of symbols in Σ, k > 1 . For an input string x x^R, let r = | x |, the length of x. Since there are k^r possible input strings x, the Petri net must have k^r distinct reachable states after r transitions in order to remember the complete string x. If we do not have this many states, then for some strings x₁ and x₂ we have δ ( μ, x₁ ) = δ ( μ, x₂ ) for x₁ ≠ x₂. Then we see that

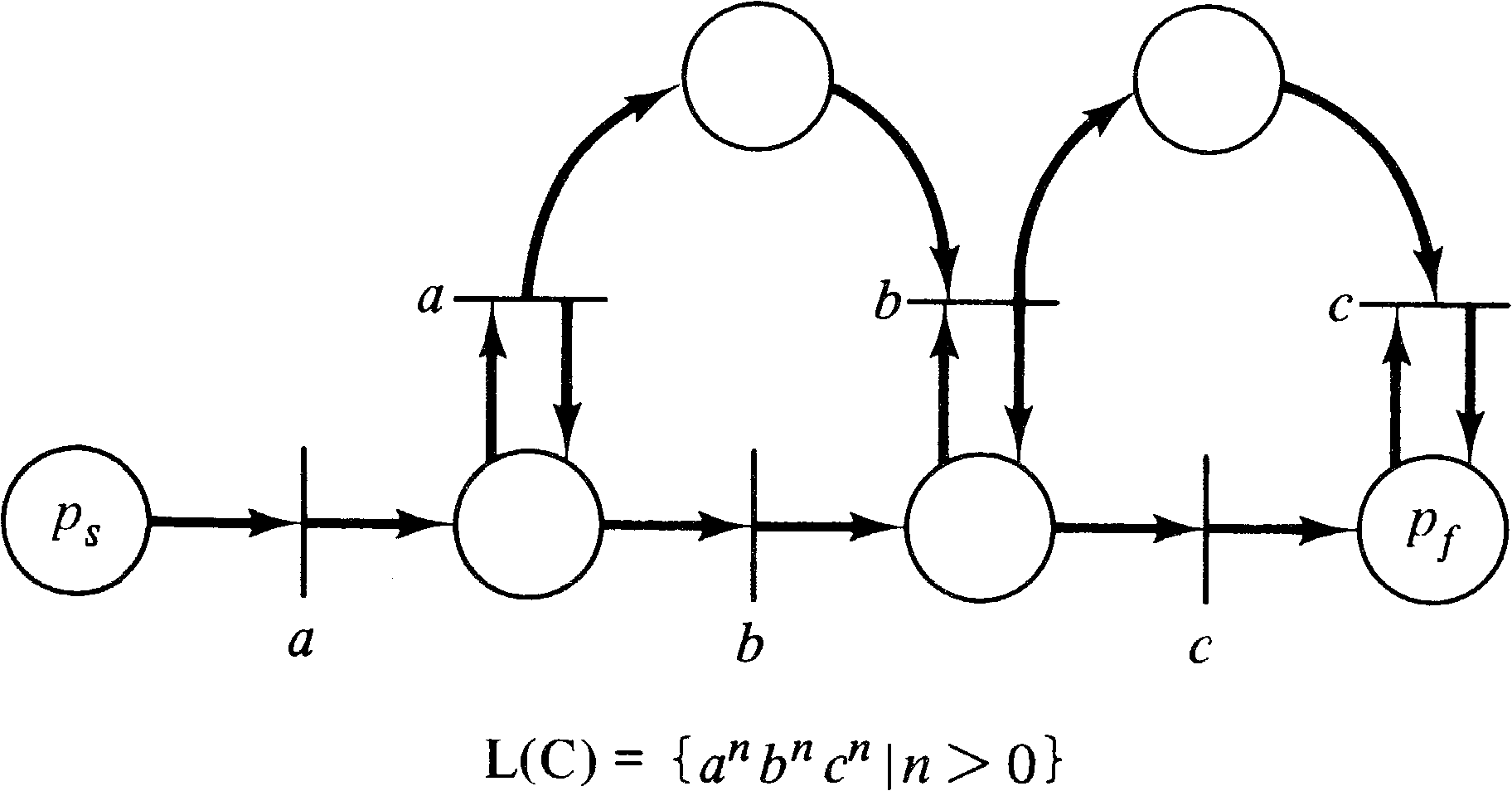
δ(μ, x1 x2R)	=	δ(δ(μ, x1), x2R)
	=	δ(δ(μ, x2), x2R)
	=	δ(μ, x2 x2R) ∈ F

and the Petri net will incorrectly generate x₁ x₂^R.

In Section 4.2.2, we showed that for each transition t_j there exists a vector v_j = e [ j ] ⋅ D such that if δ ( q, t_j ) is defined, then the value of δ ( q, t_j ) is q + v_j. Thus after r inputs, we have a state q_r where

qr	=	μ +	Σ	vij
			j

for a sequence of transitions t_i1 t_i2... t_ir. Another way of expressing this sum is as

qr	=	μ +	Σ	fj vj
			j

where f_j is the number of times transition t_j occurs in the sequence t_i1 t_i2... t_ir [ f = ( f₁, f₂, …, f_m ) is the firing vector]. We also have the constraint that

Σ	fj	=	r
j

At best the vectors v₁, v₂, …, v_m will be linearly independent, and each firing vector ( f₁, f₂, …, f_m ) will represent a unique state q_r. Since the sum of the coefficients is r, the vector ( f₁, f₂, …, f_m ) is a partition of the integer r into m parts. Knuth [1973] has shown that the number of partitions of an integer r into m parts is

&leftbigparen;

r + m − 1

m − 1

&rightbigparen;
Now since

&leftbigparen; r + m − 1 m − 1 &rightbigparen;

=

(r + m − 1) ⋯ (r + 1) (m − 1)!

<

(r + m)m

there are strictly less than ( r + m )^m reachable states in the reachability set after r inputs. For large enough r, we have then that

&leftbigparen;

---

m − 1

r + m − 1

&rightbigparen; < { ( r + m )^m } < k^r
and it is impossible for there to be k^r distinct states for each of the k^r possible input strings. Thus, it is impossible for a Petri net to generate the language w w^R. Q.E.D.

The proof that w w^R is not a Petri net language sheds some light on the limitations of Petri nets as automata and hence on the nature of Petri net languages. Petri nets are not capable of remembering arbitrarily long sequences of arbitrary symbols. From the proof, we see that Petri nets can remember sequences of bounded length (but so can finite state machines). Another feature of Petri nets is the ability to remember the number of occurrences of a symbol, such as in aⁿ bⁿ cⁿ, to an extent that regular and context-free generators cannot. However, a Petri net cannot simulate the power of a pushdown stack, which is necessary to generate context-free languages. The rate of growth of the reachable state space for a Petri net is combinatorial with the length of the input and not exponential as needed for a pushdown stack.

The reason that Petri nets are able to generate languages which a pushdown stack cannot generate despite the smaller state space is because of the more flexible interconnections between states in the Petri net compared to the restrictive paths between states allowed in a pushdown stack automaton. This results from restricting the pushdown stack automaton to accessing only the top of the stack, while the Petri net can access any of its counters at any time.

Having shown that not all context-free languages are Petri net languages and not all Petri net languages are context-free, the question arises as to what is the class of languages which are both context-free and Petri net languages? At present we cannot fully answer this question, but we can give an indication of some of the members of this intersection. One subset of both context-free and Petri net languages is, of course, the class of regular languages. Another subset is the set of bounded context-free languages investigated by Ginsburg [1966].

6.6.3. Bounded Context-free Languages

A context-free language L is bounded context-free if there exist words (or strings) w₁, w₂, …, w_m from Σ^* such that

Bounded context-free languages are characterized by the following theorem of Ginsburg [1966, Theorem 5.4].

THEOREM 6.10

The family of bounded context-free languages is the smallest family of sets defined by

1. If W is a finite subset of Σ^*, then W is bounded context-free.

2. If W₁ and W₂ are bounded context-free, then W₁ ∪ W₂ and W₁W₂ are bounded context-free.

3. If W is bounded context-free and x, y ∈ Σ^*, then { xⁱ W yⁱ | i ≥ 0 } is bounded context-free.

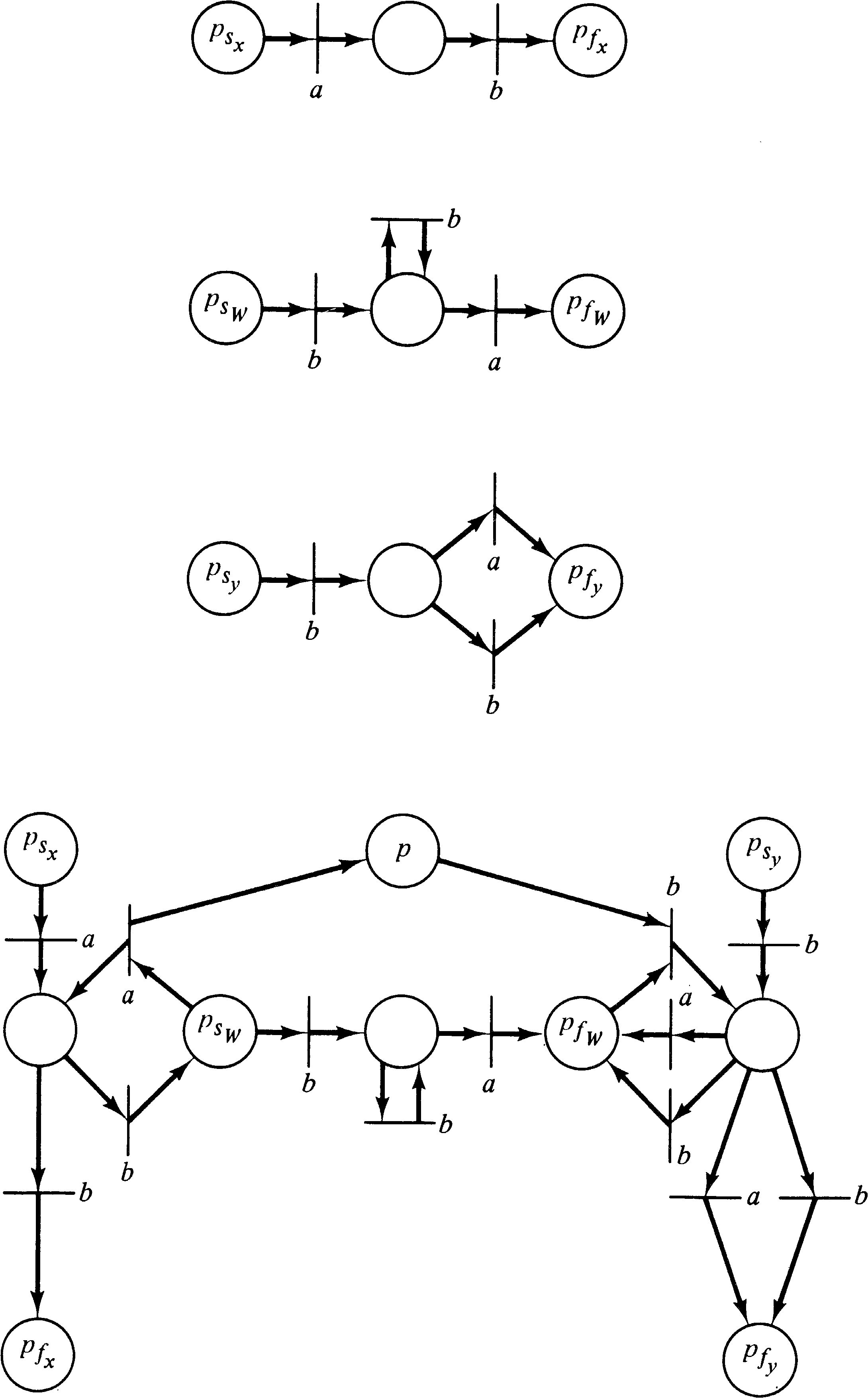
We have already shown (Section 3.3.1) that every finite state machine and hence every regular language and every finite subset of Σ^* is a Petri net language. In Sections 6.5.1 and 6.5.2 we showed that Petri net languages are closed under concatenation and union. Thus we have only to show that 3 above is satisfied for Petri net languages. To show this, we would construct a Petri net γ′ = (C′, Σ, μ′, F′ ) which generates the Petri net language { xⁱ W yⁱ | i ≥ 0 } given standard form Petri nets γ_x = (C_x, Σ, μ_x, F_x ), γ_y = (C_y, Σ, μ_y, F_y ), and γ_W = (C_W, Σ, μ_W, F_W ) that generate x, y, and W, respectively. γ′ combines the Petri nets γ_x, γ_y, and γ_W and a new place p so that each time γ_x is executed, a token is placed in p. The place p counts the number of times γ_x is executed. After γ_x has executed as many times as it wishes, γ_W is executed, and finally γ_y is executed repeatedly, removing one token from p for each repetition. Since the input string is correctly generated only if the Petri net is empty (except for F′ which is defined to be F_y ), we are assured that the number of executions of γ_x and γ_y are equal.

This construction, which is demonstrated in Figure 6.14, for x = a b, y = b ( a + b ), and W = b⁺ a, shows that { xⁱ W yⁱ | i ≥ 0 } is a Petri net language. Thus any bounded context-free language is a Petri net language.

Are there context-free languages which are also Petri net languages but not bounded? Unfortunately, the answer is yes. Ginsburg shows that the regular expression ( a + b )⁺ is not a bounded context-free language. Since this language is a context-free Petri net language, we see that bounded context-free languages are only a proper subset of the family of context-free Petri net languages. We also exhibit the language { ( a + b )⁺ aⁿ bⁿ | n > 1 } which is a context-free Petri net language but is neither bounded nor regular. Further research is needed to completely characterize the set of context-free Petri net languages.

The presence of both regular sets and bounded context-free languages as subsets of the class of Petri net languages is encouraging since both classes of languages have several desirable properties and some nice analysis characteristics.

6.6.4. Context-sensitive Languages

We have investigated the relationship between Petri net languages and regular languages and between Petri net languages and context-free languages. Now we turn to context-sensitive languages. Figure 6.13 has shown that some Petri net languages are context-sensitive; below we prove that all Petri net languages are context-sensitive. Since we know that all context-free languages are also context-sensitive and that there exist context-free languages which are not Petri net languages, we know that there exist context-sensitive languages which are not Petri net languages. Thus the inclusion is proper.

THEOREM 6.11

All Petri net languages are context-sensitive languages.

The proof that all Petri net languages are context-sensitive is rather complex. There are two ways to show that a language is context-sensitive: Construct a context-sensitive grammar which generates it, or specify a nondeterministic linear bounded automaton which generates it. Peterson [1973] has shown how to define a context-sensitive grammar to generate a Petri net language; here we indicate why a linear bounded automaton can generate a Petri net language.

A linear bounded automaton is similar to a Turing machine. It has a finite state control, a read/write head, and a (two-way infinite) tape. The limiting feature which distinguishes it from a Turing machine is that the amount of tape which can be used by a linear bounded automaton to generate a given input string is bounded by a linear function of the length of the input string. In this sense it is similar to the pushdown stack automaton used to generate context-free languages (since the maximum length of the stack is bounded by a linear function of the input string) except that the linear bounded automaton has random access to its memory, while the pushdown automaton has access to only one end of its memory.

To generate a Petri net language, one can simulate the Petri net by remembering, after each input, the number of tokens in each place. How fast can the number of tokens grow as a function of the input? Consider the number of tokens after r transition firings. This number, denoted by c, is, for a transition sequence t_i1 t_i2... t_ir,

With this proof, we have shown that all Petri net languages are context-sensitive languages. We summarize the results of our investigation into the relationship between the class of Petri net languages and other classes of languages in the graph and Venn diagram of Figure 6.15.

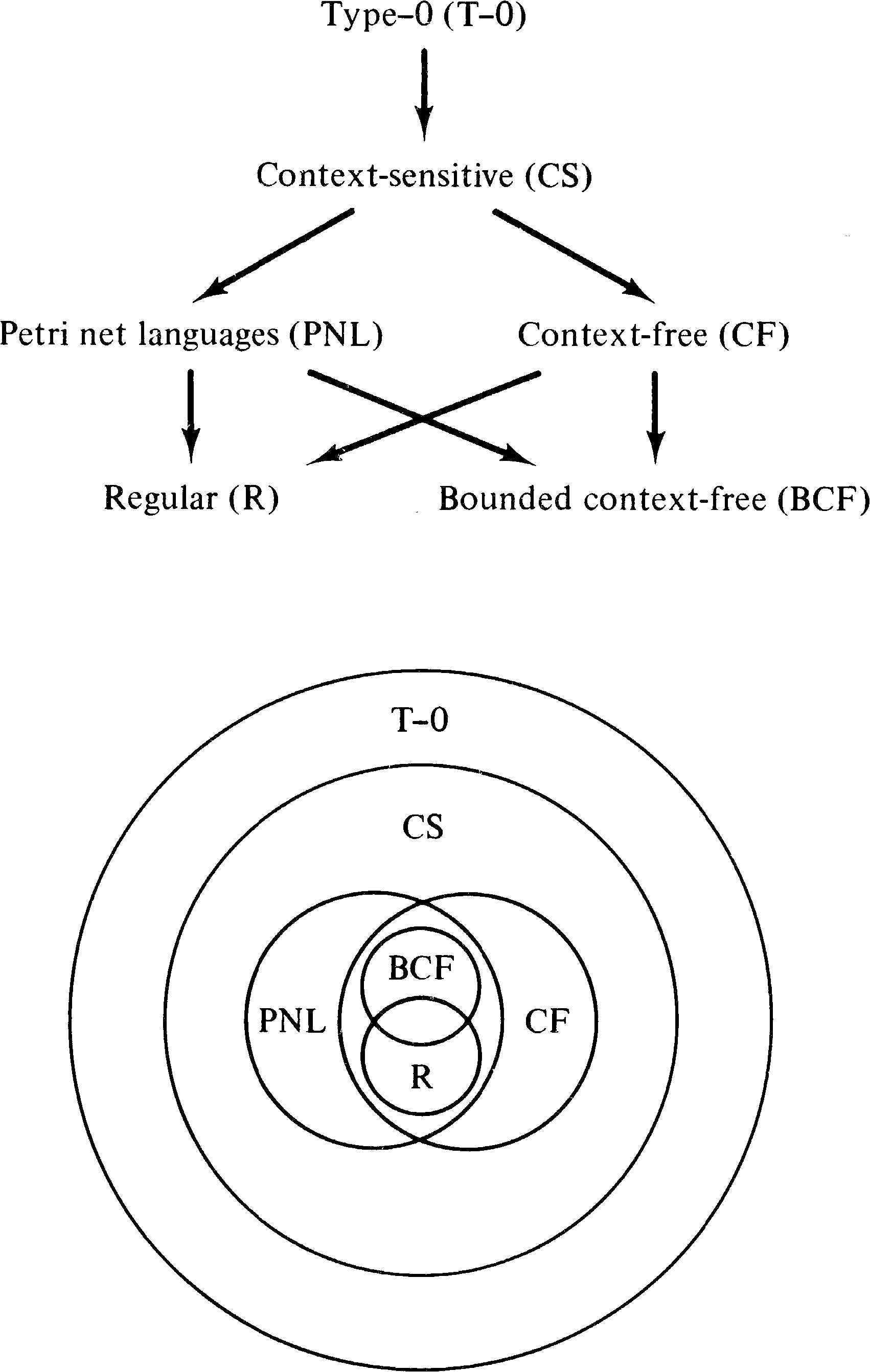
Figure 6.16 summarizes the properties of Petri net languages. It is drawn from [Peterson 1976] and [Hack 1975b].

Most of the results presented here have been developed in both [Peterson 1976] and [Hack 1975b]. In addition, Hack has investigated a number of decidability problems for Petri net languages. The membership problem [Is a string α an element of a language L ( γ ) ?] is decidable, while the emptiness problem [Is the language L ( γ ) empty?] can be easily seen to be equivalent to the reachability problem. It is undecidable if two Petri net languages are equal or if one is contained within the other (the equivalence and inclusion problems).

Figure 6.17 summarizes these results.

A different approach to the study of Petri nets by the use of formal language theory has been considered by Crespi-Reghizzi and Mandrioli [1974]. They noticed the similarity between the firing of a transition and the application of a production in a derivation, thinking of places as nonterminals and tokens as separate instances of the nonterminals. The major difference is, of course, the lack of ordering information in the Petri net which is contained in the sentential form of a derivation. This resulted in the definition of the commutative grammars, which are isomorphic to Petri nets. In addition Crespi-Reghizzi and Mandrioli considered the relationship of Petri nets to matrix [Abraham 1970], scattered context, nonterminal bounded, derivation bounded, equal-matrix, and Szilard languages. For example, it is not difficult to see that the class L^f is the set of Szilard languages of matrix context-free languages [Crespi-Reghizzi and Mandrioli 1977; Hopner and Opp 1977].

6.8. Further Reading

There are three good studies on Petri net languages. [Peterson 1976] or [Peterson 1977] is probably the easiest to get, although [Hack 1975b] is a more rigorous and complete investigation. [Crespi-Reghizzi and Mandrioli 1974] is rather hard to find, but nonetheless it is an excellent piece of work, quite inventive and well explained.

6.9. Topics for Further Study

Although a good start on research into the properties of Petri nets has been made, much still remains to be done. Of the classes of languages which have been defined, only two, the classes of P-type and L-type languages, have been studied and these only for generalized Petri nets. Several subsets of the set of general Petri nets have been defined, including marked graphs, conflict-free nets, restricted nets, and free-choice nets, as we see in Chapter 7. Each of these classes of Petri nets presumably has its own class of languages with its own distinctive properties. Some investigation of these classes has been done. It is known [Hack 1975b] that the classes L, L^λ, G, G^λ, P, and P^λ for restricted Petri nets [no self-loops, no multiple arcs; i.e., all bags are sets, and for every t_j, I ( t_j ) ∩ O ( t_j ) = ∅ ] are identical to the corresponding classes for generalized Petri nets. It is also not difficult to see that the classes L^λ, G^λ, and P^λ are not changed by restricting the nets to free-choice nets (see Section 7.4.3). This still leaves many interesting cases to be studied. In particular, the languages generated by marked graphs, or by conflict-free nets in general, seem to have a structure reminiscent of deterministic context-free languages, and their study should be very promising.

Another important open problem concerns the distinction between λ -free languages ( L, P, …) and unrestricted languages ( L^λ, P^λ, …). It is not known whether L = L^λ or not, for example.

1. Pick a class of Petri net languages other than the L-type languages and develop its theory.

2. Develop a complete set of interrelations between the 12 classes of Petri net languages. Specifically, for each pair of Petri net language classes, either show that one class is contained in another, or exhibit a language which is in one class and not in the other.

3. Consider the possibility of associating labels with the places of a Petri net, not the transitions. This was the approach used in [Gostelow 1971]. Determine the feasibility of this approach, and if feasible, develop a new theory of Petri net place languages.

4. Develop the theory of Petri net languages where Petri nets are considered to be recognizers, not generators, of the language.