Chapter 1. Introduction

Petri nets are a tool for the study of systems. Petri net theory allows a system to be modeled by a Petri net, a mathematical representation of the system. Analysis of the Petri net can then, hopefully, reveal important information about the structure and dynamic behavior of the modeled system. This information can then be used to evaluate the modeled system and suggest improvements or changes. Thus, the development of a theory of Petri nets is based on the application of Petri nets in the modeling and design of systems.

1.1. Modeling

The application of Petri nets is through modeling. In many fields of study, a phenomenon is not studied directly but indirectly through a model of the phenomenon. A model is a representation, often in mathematical terms, of what are felt to be the important features of the object or system under study. By the manipulation of the representation, it is hoped that new knowledge about the modeled phenomenon can be obtained without the danger, cost, or inconvenience of manipulating the real phenomenon itself. Examples of the use of modeling include astronomy (where models of the birth, death, and interaction of stars allow studying theories which would take long times and massive amounts of matter and energy), nuclear physics (where the radioactive atomic and subatomic particles under study exist for very short periods of time), sociology (where the direct manipulation of groups of people for study might cause ethical problems), biology (where models of biological systems require less space, time, and food to develop), and so on.

Most modeling uses mathematics. The important features of many physical phenomena can be described numerically and the relations between these features described by equations or inequalities. Particularly in the natural sciences and engineering, properties such as mass, position, momentum, acceleration, and forces are describable by mathematical equations. To successfully utilize the modeling approach, however, requires a knowledge of both the modeled phenomena and the properties of the modeling technique. Thus, mathematics has developed as a science in part because of its usefulness in modeling the phenomena of other sciences. For example, the differential calculus was developed in direct response to the need for a means of modeling continuously changing properties, such as position, velocity, and acceleration in physics.

The development of high-speed computers has greatly increased the use and usefulness of modeling. By representing a system as a mathematical model, converting that model into instructions for a computer, and running the computer, it is possible to model larger and more complex systems than ever before. This has resulted in considerable study of computer modeling techniques and of computers themselves. Computers are involved in modeling in two ways: as a computational tool for modeling and as a subject of modeling.

1.2. Features of Systems

Computer systems are very complex, often large, systems of many interacting components. Each component can be quite complex, as can its interactions with other components in the system. This is also true of many other systems. Economic systems, legal systems, traffic control systems, and chemical systems all involve many individual components interacting with other components, possibly in complex ways.

Thus, despite the diversity of systems which we want to model, several common points stand out. These should then be features of a useful model of these systems. One fundamental idea is that systems are composed of separate, interacting components. Each component may itself be a system, but its behavior can be described independently of other components of the system, except for well-defined interactions with other components. Each component has its own state of being. The state of a component is an abstraction of the relevant information necessary to describe its (future) actions. Often the state of a component depends on the past history of the component. Thus the state of a component may change over time. The concept of “state” is very important to modeling a component. For example, in a queueing system model of a bank, there may be several tellers and several customers. The tellers may be either idle (waiting for a customer to need service) or busy (serving a customer). Similarly, the customers may be idle (waiting for a teller to be free to serve them) or busy (being served by a teller). In a model of a hospital, the state of a patient might be critical, serious, fair, good, or excellent.

The components of a system exhibit concurrency or parallelism. Activities of one component of a system may occur simultaneously with other activities of other components. In a computer system, for example, peripheral devices, such as card readers, line printers, tape drives, and so on, may all operate concurrently under the control of the computer. In an economic system, manufacturers may be producing some products while retailers are selling other products, and consumers are using still other products, all at the same time.

The concurrent nature of activity in a system creates some difficult modeling problems. Since the components of the systems interact, it is necessary for synchronization to occur. The transfer of information or materials from one component to another requires that the activities of the involved components be synchronized while the interaction is occurring. This may result in one component waiting for another component. The timing of actions of different components may be very complex and the resulting interactions between components difficult to describe.

1.3. The Early Development of Petri Nets

Petri nets are designed specifically to model these types of systems: systems with interacting concurrent components. Petri nets have been developed from the early work of Carl Adam Petri [1962a]. In his doctoral dissertation, “Kommunikation mit Automaten,” [Communication with automata], Petri formulated the basis for a theory of communication between asynchronous components of a computer system. He was particularly concerned with the description of the causal relationships between events. His dissertation was mainly a theoretic development of the basic concepts from which Petri nets have developed.

The work of Petri came to the attention of A. W. Holt and others of the Information System Theory Project of Applied Data Research, Inc. (ADR). Much of the early theory, notation, and representation of Petri nets developed from the work on the Information System Theory Project and was published in the final report of that project [Holt, et al 1968] and in a separate report entitled “Events and Conditions” [Holt and Commoner 1970]. This work showed how Petri nets could be applied to the modeling and analysis of systems of concurrent components.

Petri's work also came to the attention of Project MAC at the Massachusetts Institute of Technology (M.I.T.). The Computation Structures Group, under the direction of Professor Jack B. Dennis, has been the source of considerable research and publication on Petri nets, publishing several Ph.D. dissertations and numerous reports and memos (see the bibliography). Two important conferences on Petri nets have been held by the Computation Structures Group: the Project MAC Conference on Concurrent Systems and Parallel Computation in 1970 at Woods Hole [Dennis 1970b] and the Conference on Petri Nets and Related Methods in 1975 at M.I.T.. Both of these conferences have helped to disseminate results and approaches in Petri net theory.

The use and study of Petri nets has spread widely in the last few years. A workshop on Petri nets was held in Paris in 1977 and an advanced course on General Net Theory in Hamburg in 1979. A special interest group on Petri nets has been formed in Germany. Research in and application of Petri nets is becoming widespread.

1.4. Applying Petri Net Theory

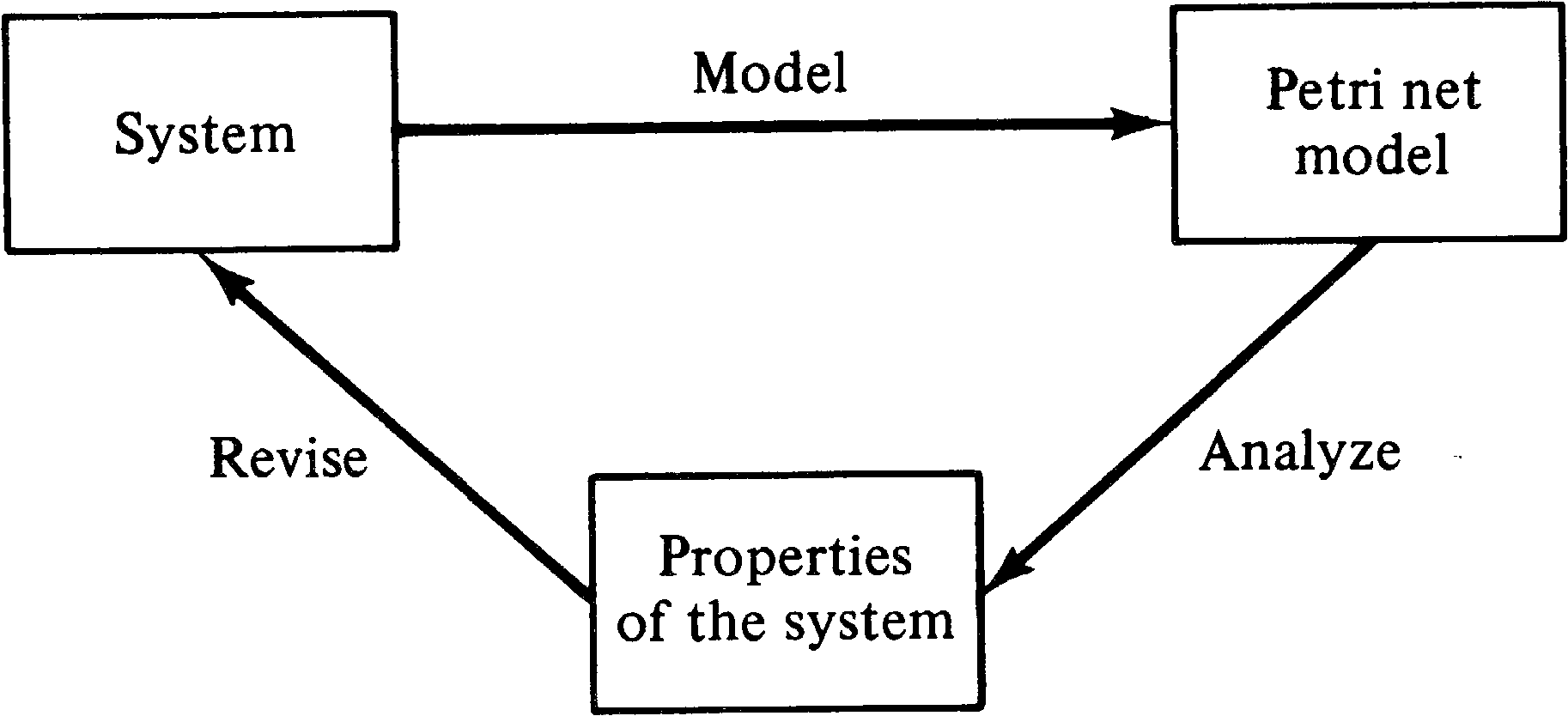
The practical application of Petri nets to the design and analysis of systems can be accomplished in several ways. One approach considers Petri nets as an auxiliary analysis tool. For this approach, conventional design techniques are used to specify a system. This system is then modeled as a Petri net and this Petri net model is analyzed. Any problems encountered in the analysis point to flaws in the design. The design must be modified to correct the flaws. This modified design can then be modeled and analyzed again. This cycle is repeated until the analysis reveals no unacceptable problems. This approach is diagrammed in Figure 1.1. Note that this approach can also be used to analyze an existing, currently operational system.

The conventional approach described above for using Petri nets in the design of a system requires constant conversion between the designed system and the Petri net model. An alternate approach has been suggested. In this more radical approach, the entire design and specification process is carried out in terms of Petri nets. Analysis techniques are applied only as necessary to create a Petri net design which is error-free. Then the problem is to transform the Petri net representation into an actual working system.

These two approaches to using Petri nets in the design process provide different types of problems for the Petri net researcher. In the first case, modeling techniques must be developed to transform systems into a Petri net representation; in the second case, implementation techniques must be developed to transform Petri net representations into systems. In both cases, we need analysis techniques to determine the properties of our Petri net model. Thus, our primary concern in the development of a theory of Petri nets is to study the properties of the Petri nets themselves.

1.5. Applied and Pure Petri Net Theory

The study of Petri nets has developed in two directions: Applied Petri net theory is concerned mainly with the application of Petri nets to the modeling of systems, the analysis of these systems, and the resulting insights into the modeled system. Successful work in this area requires a good knowledge of the application area and of Petri nets and Petri net techniques.

Pure Petri net theory is the study of Petri nets to develop the basic tools, techniques and concepts needed for the application of Petri nets. Although the motivation for Petri net research is based on applications, there is a need for a firm foundation of Petri net theory to be able to apply Petri nets. Much of the work on Petri nets at this point has concentrated on the fundamental theory of Petri nets, developing the tools and approaches which may someday be useful in the application of Petri nets to specific real-world problems. In this book, we present some of both areas of Petri net theory (pure and applied) but concentrate mainly on the basic theory. The applications which are given are intended mainly to demonstrate the versatility and power of Petri nets and to motivate the development of the analysis techniques.

We do not attempt to cover the entire range of Petri net topics in depth but rather hope to provide a firm foundation in terms, concepts, approaches, results, and history of Petri nets to allow a computer scientist or graduate student to be able to use and understand the growing body of Petri net literature and to be able to apply this theory to an even wider range of applications. We begin with some formal definitions and examples of Petri nets in Chapter 2 and then proceed with demonstrating their power and usefulness in the remainder of the book. The annotated bibliography provides references to most work on Petri nets.

1.6. Further Reading

The birth of Petri nets was Petri's dissertation [Petri 1962a], but most work in the United States is also based on the final report of the Information System Theory Project [Holt, et al 1968] which translated Petri's dissertation into English as well as extending the work considerably. The “Events and Conditions” paper by Holt and Commoner [1970] is also an important part of the early works. Petri presented a short paper to the 1962 IFIP Congress which was printed in the proceedings [Petri 1962b]. This paper is based on the ideas in his dissertation.

The approach presented in this book derives largely from the work of the Computation Structures Group at M.I.T. and has developed from the work of Dennis [1970a], Patil [1970a], and others, culminating in the work of Hack [1975c]. Keller has also been influential with his report on vector replacement systems [Keller 1972] and his view of modeling [Keller 1975a].

1.7. Topics for Further Study

1. Trace the origin and flow of the important ideas in Petri net theory. The starting point is most obviously Petri, but how did the ideas flow to the United States and to whom? How did they flow from there? Use published reports, papers, dissertations, and memos to determine precedence by date and citations in their references. You will probably want to interview some of the key people: Petri, Holt, Dennis, Patil, and so on.