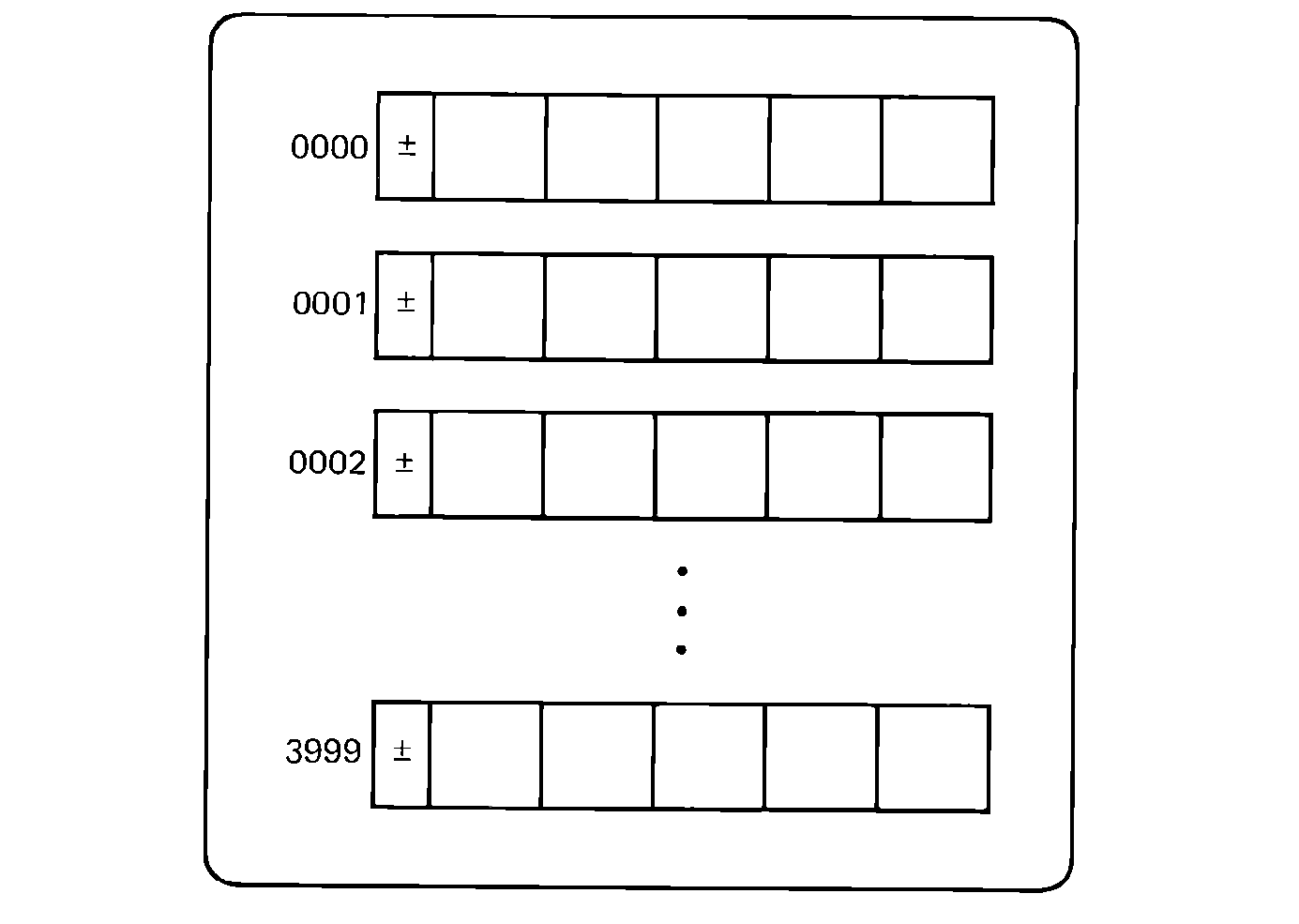
FIGURE 2.1 The MIX memory (4000 words; 5 bytes plus sign).
The MIX computer system first appeared in 1968, although prototype models were undoubtedly in use before this. The MIX machine was designed to be both powerful and simple. It incorporates many of the useful and common features of a large class of computers. Although you may never have an opportunity to program in MIX machine language after this text, the MIX machine is so similar to many other computers that you will be able to learn and program the machine language for any new computer easily if you are able to program well for the MIX computer.
Although we will talk about the MIX computer, there is not just one MIX computer, but rather a family of computers. The basic machine, the MIX 1009, is available in a number of models. The choice of which model should be used is an important decision and is affected by the problems for which the computer will be programmed and the funds available (the bigger models cost more). All MIX machines have the same basic instruction set and architecture. This basic machine is the MIX 1009. To this basic machine can be added I/O devices, additional memory, and additional instructions to increase the speed, capacity, and convenience of the basic machine. We shall introduce some of these extensions as we discuss the MIX machine, in order to show how the capabilities of the machine can be increased. Most of our discussion is applicable to all MIX computers, with one exception.
The original design of the MIX machine reveals a certain ambiguity as to whether it is a binary machine or a decimal machine. This is to its credit, since, as we have seen, both systems have their advantages and disadvantages. With the rapid technological changes which are occurring in the design and use of computer hardware, a machine which is too closely tied to a particular hardware technology may rapidly become obsolete. The MIX machine was designed to be a flexible computer which can be implemented in many different hardware technologies. Thus, it will be able to evolve and improve while maintaining compatibility of programs which are written for different models of the computer. Most programs can be written so that they will work properly on any MIX machine, be it binary, decimal, hexadecimal, or any other underlying number system. MIX programs should be written to execute correctly for a variety of memories, computation units, and I/O devices.
There are certain properties of a specific model of the MIX machine which can be exploited, however, to increase considerably the efficiency and clarity of a program. It is important, for example, that the techniques for handling binary data be well understood, since so many computers are binary. Because of these considerations, we will sometimes use, not the basic MIX 1009 computer, but the MIX 1009B binary computer for our examples.
The MIX 1009B is a binary MIX computer with the same basic architecture as the MIX 1009, but with an explicitly binary representation of instructions and data. The instruction set has been extended to include instructions which exploit the binary data representation. These instructions are seldom needed, so most programs for the MIX 1009B computer will execute correctly on the MIX 1009D decimal computer as well as the basic MIX 1009 computer. Programs which use only the instructions which are available on all three machines are using the common instruction set. We state when the binary nature of the MIX 1009B computer is used in any of our programs.
A considerable amount of our early discussion of the MIX computer will deal with the representation of data and instructions in the computer. Since more computers represent information in binary than in decimal, we will likewise use binary to show our data representations. The contents of memory and encodings will thus be presented in binary (octal, actually).
We turn now to examining the basic architecture of the MIX computer. The presentation of the specific properties of the MIX computer follows the general presentation of Chapter 1. We consider first the memory unit and registers of the MIX machine, its number representation scheme, its input/output system, character code, and instruction set. After a brief introduction to the instruction set, we turn to a description of the MIXAL assembly language for the MIX computers. Chapter 3 presents a very detailed discussion of the instruction set for the MIX computer.
The basic MIX machine has 4000 words of memory. These are addressed by the addresses 0, 1, 2, …, 3999. Each word of memory consists of five bytes plus a sign. Each byte is six bits (on a binary machine). Thus, a MIX word is 31 bits, consisting of a one-bit sign and 5 six-bit bytes. Bytes are numbered from 0 to 5, left to right, with "byte" 0 being the sign bit.
| sign | byte | byte | byte | byte | byte | |
| Byte | 0 | 1 | 2 | 3 | 4 | 5 |
The MIX machine has nine registers. The A (accumulator) register and the X (extension) register are both five bytes plus sign, like the words of memory. The A register is called rA; the X register, rX. Six index registers are named I1, I2, I3, I4, I5, I6. Index registers are only two bytes plus sign. The J (jump) register is only two bytes and is identified by rJ. In addition to these nine registers, the MIX machine has an overflow toggle (OT) and a comparison indicator (CI). The overflow toggle is one bit, being either ON or OFF, while the comparison indicator has three states: LESS, EQUAL, and GREATER. The usage of these registers will become clear later.
FIGURE 2.1 The MIX memory (4000 words; 5 bytes plus sign).
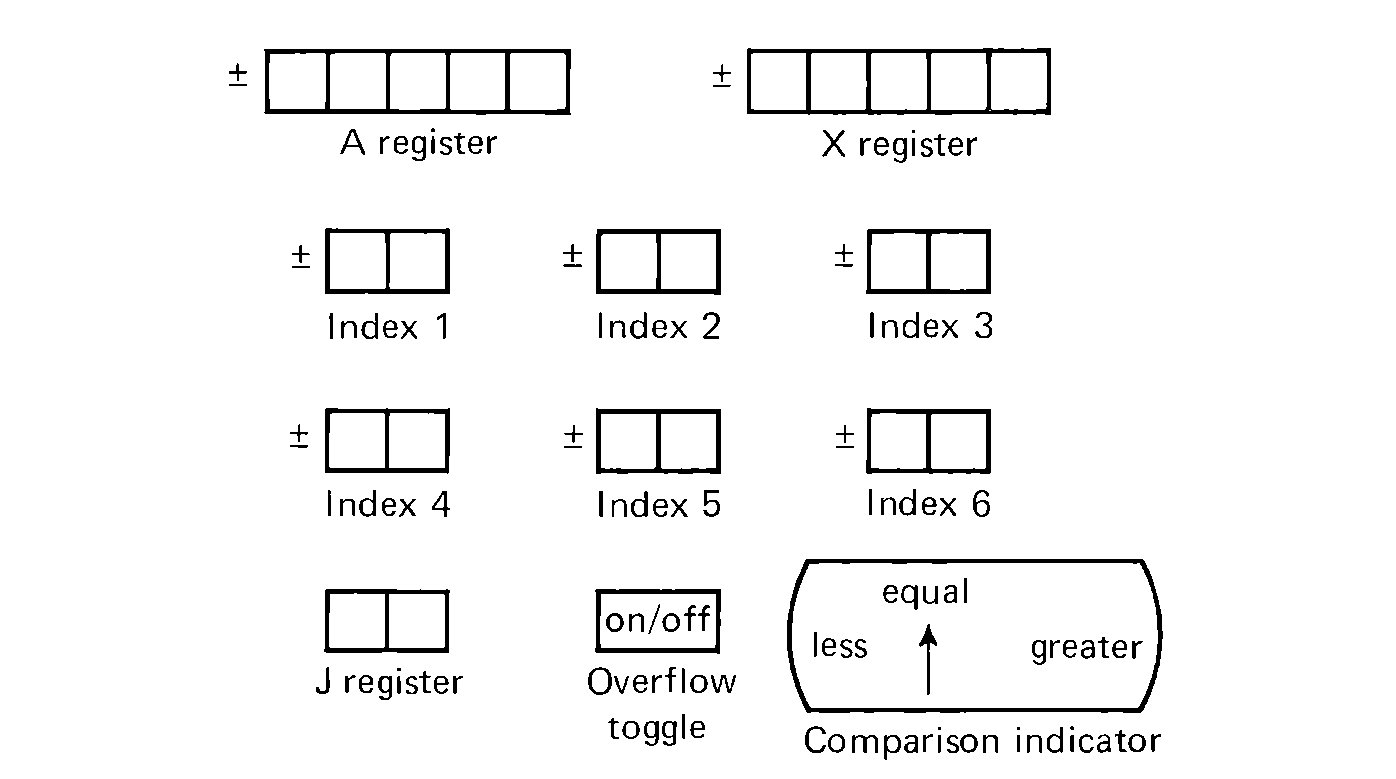FIGURE 2.2 The MIX registers.
Numbers are represented in sign and magnitude notation. With six bits per byte
| one byte | can represent | 0 through 63. |
| two bytes | can represent | 0 through 4095. |
| three bytes | can represent | 0 through 262,143. |
| four bytes | can represent | 0 through 16,777,215. |
| five bytes | can represent | 0 through 1,073,741,823. |
Floating point numbers are represented by storing a biased (excess 32) base 64 exponent in byte 1 (the high-order byte) and the fractional part in bytes 2 through 5. The MIX word
| ± | e | f1 | f2 | f3 | f4 |
| ±0.f1f2f3f4 | × | 64 e-32 |
Double precision floating point numbers on the MIX computer extend both the range and accuracy of representation by using two MIX words as
| ± | e1 | e2 | f1 | f2 | f3 | ± | f4 | f5 | f6 | f7 | f8 |
| ±0.f1f2f3f4f5f6f7f8 | × | 64 e1e2-2048 |
The sign of the number is determined by the sign of the first word; the sign bit of the second word is ignored. This representation gives about 12 places of accuracy and a range from approximately 10-3700 to 103700.
The MIX machine has provision for several different input/output devices. The basic MIX machine has room for up to 20 separate devices. These are nominally used for eight magnetic tape units, eight disk or drum units, a card reader, a card punch, a line printer, and a typewriter/ paper tape device. Each device is identified by a unit number from 0 to 19. This corresponds to the slot in the MIX computer chassis in which the interface card for the device is plugged in. The disks, drums, and tapes store information in 100-word fixed length records. The card reader, card punch, line printer, and typewriter/paper tape units are character oriented and use the MIX character code shown in Table 2.1. Each byte of a MIX word can store one character, so each word can store 5 characters. The card reader and card punch have 16 word (80 character) records, while the line printer uses 24 words per record (120 characters). The typewriter/paper tape unit transmits 70 characters (14 words) at a time.
| Character | MIX | Character | MIX | Character | MIX | Character | MIX |
| blank | 00 | M | 14 | Y | 28 | ( | 42 |
| A | 01 | N | 15 | Z | 29 | ) | 43 |
| B | 02 | O | 16 | 0 | 30 | + | 44 |
| C | 03 | P | 17 | 1 | 31 | - | 45 |
| D | 04 | Q | 18 | 2 | 32 | * | 46 |
| E | 05 | R | 19 | 3 | 33 | / | 47 |
| F | 06 | Φ | 20 | 4 | 34 | = | 48 |
| G | 07 | Π | 21 | 5 | 35 | $ | 49 |
| H | 08 | S | 22 | 6 | 36 | < | 50 |
| I | 09 | T | 23 | 7 | 37 | > | 51 |
| Θ | 10 | U | 24 | 8 | 38 | @ | 52 |
| J | 11 | V | 25 | 9 | 39 | ; | 53 |
| K | 12 | W | 26 | . | 40 | : | 54 |
| L | 13 | X | 27 | , | 41 | ' | 55 |
The instruction set of the MIX machine is represented in the following format
| ± | A | A | I | F | C |
There are eight classes of instructions for the MIX machine. Loading Operators copy information from memory into the registers, while the storing operators copy from the registers back to memory. These are necessary because all arithmetic operations operate on the registers. A set of immediate operators allow the registers to be modified by small constants. Data can be tested by a set of comparison operators which set the comparison indicator. Jump instructions can transfer control to different instructions based upon the comparison indicator or the state of the registers. Input/Output operations allow information to flow between memory and the input/output devices. A set of miscellaneous operations includes instructions to move information from memory to memory, shift information in the registers, and convert between the character code and binary representation of numbers.
An assembly language or machine language programmer must be very familiar with the instruction set of the machine which is being used. However, often some of the instructions are used only rarely, in certain special circumstances. Some instructions may also be rather complex. Because of this an assembly language programmer always programs with a computer reference manual at hand. The computer reference manual lists all the instructions for the computer and exactly what they do. In Chapter 3, we give a reference manual for the MIX computer. This is a rather technical and lengthy description of the MIX instruction set and may require several readings before it is completely understood. This is normal. Whenever you are programming, you may want to refer to the description of the MIX instruction set often.
Each instruction is specified by its numeric opcode (C) and the opcode modifier (F). The computer hardware interprets the contents of the C and F fields of the instruction and performs the instruction specified. Thus, if the opcode is 10 (octal) and the F field is 05, then the hardware knows that it is to take the contents of the location specified by the address part of the instruction and copy it into the A register.
It is difficult to memorize all the different numeric opcodes of a computer and their corresponding instruction. Because of this, assembly language programmers do not use the numeric opcode of an instruction to identify the instruction but use a short name which tries to describe the effect of the instruction. This is a symbolic opcode. It is also called a mnemonic opcode. For example, the instruction which copies the contents of a memory location into the A register is denoted by "LDA" which stands for " LoaD the A register". Machine language programs are developed with symbolic opcodes, rather than numeric opcodes. After the program is written, it is necessary only to look up in a table the corresponding numeric opcode for each symbolic opcode, in order to produce the final machine language program (in binary).
The choice of which symbolic opcodes stand for which numeric opcodes is completely arbitrary. However, most symbolic opcodes are a natural abbreviation for the machine instruction in order to make them easier to remember. Also, since programmers want to be able to talk to each other about their programs, everyone who is working with a given machine generally uses the same symbolic opcodes. The symbolic opcodes are almost always assigned by the computer manufacturer and everyone uses these standard symbolic opcodes.
We give now a brief description of the MIX instruction set.
There are 16 loading operators. These loading operators are used to copy the contents of a memory location (or the negative of the contents) into the registers of the MIX machine. The address of the location to be copied from is specified by the address part of the instruction. There is a separate instruction to allow loading of the A register, the X register, and the six index registers, and another separate instruction for loading the negative of the contents of a memory location into each of these eight registers.
In addition to being able to load from memory into the registers, we need to be able to store information from the registers into memory. The storing operators allow this to be done. These storing operators are almost the opposite of the loading operators. The contents of the A register, the X register, and the six index registers can be stored into any memory location. In addition to these instructions, we can also store the J register. Another special store instruction allows us to easily set any memory location to zero, a very important value in programming.
Being able to move information between memory and the registers is of little use if we cannot do useful computations with the information. The arithmetic operators provide the four standard arithmetic operations of addition, subtraction, multiplication and division for both integers (ADD, SUB, MUL, DIV) and floating point numbers (FADD, FSUB, FMUL, FDIV). These operations are all binary operations; that is, they operate on two operands. But notice that we have only one address per instruction, and hence we can only specify one operand per instruction. This problem is resolved by defining all arithmetic operations to perform their operation on the A register and the memory location given in the instruction, leaving their result in the A register. Thus, an ADD instruction adds the contents of the memory location specified by the address part of the instruction to the A register, and the sum is left in the A register. The A register is often called the accumulator because of this.
In addition to being able to modify the A register by full-word addition and subtraction, it is often desirable to be able to modify the A register, the X register, and index registers by "small" integers. Commonly, it is necessary to add or subtract 1, for example. This capability can, of course, be achieved by storing a word in memory whose contents are an integer 1, and then adding or subtracting by using ADD or SUB, but the MIX machine provides a more convenient method with its immediate operators. For the normal arithmetic operators, the address field of the instruction specifies the address of a location in memory whose contents are the operand for the instruction. These operations are called memory reference instructions. With immediate operators, the address field specifies the operand itself. This means that the operand must be the same size as an address, so it is limited to being in the range -4095 to +4095, a "small" integer. Immediate operators allow the operand to be entered directly into the A, X, or index registers; or for the negative of the operand to be entered (in analogy to the "load" and "load negative" instructions) or for the operand to be added (an increment) or subtracted (a decrement) from the registers.
In addition to being able to perform computations on the registers, it is necessary in programming to be able to compare results in order to perform different computations for different types of input. The comparison operators are used to compare the contents of a register to the contents of a memory location and set the comparison indicator to indicate the result of the comparison. The comparison indicator has three possible values: LESS, EQUAL, and GREATER. The value of the comparison indicator changes only when a compare instruction is executed. There are instructions to compare a memory location to the A, X, or index registers as integers, or to the A register as a floating point number.
Once the comparison is done, we may wish to execute one of two different sequences of instructions, depending upon the result of the comparison. The jump operators allow the program to transfer control to a different location if the condition tested for is true, or to continue execution at the next location if the condition is false. Jump instructions allow the comparison indicator to be used to cause a jump, or to jump on the positive, negative, or zero state of the A, X, or index registers. Two special remarks need to be made about the jump operators. If a jump is made (for any of the jump instructions except JSJ), then the J register is set equal to the address of the instruction which immediately follows the jump instruction. This allows us to determine where we would have been if we had not jumped and is useful for subroutine calls. The JOV and JNOV instructions allow us to test the state of the overflow toggle and, in addition, always leave the overflow toggle off.
Any sequence of instructions which performs some useful computation must have input data and output results. The input/output instructions start the movement of data between the memory of the MIX computer and an external I/O device. The I/O system for the MIX machine is very simple and is controlled by only five instructions. The use of these instructions is covered in more detail in Chapter 5.
There are a few instructions that are left over, which do not fit comfortably into any of the above categories. These include operators which convert from character code to binary (NUM), and from binary to character code (CHAR), which copy a block of words starting at one location in memory to another location in memory (MOVE), and which shift the contents of the A and X registers left or right. These last instructions are the shift instructions and can shift the A register end-off, or the A and X register (as a unit) end-off or circularly. The sign bits are not affected by any of the shift instructions.
There are also a few control operations, such as HLT, which halts the computer, and NOP, which does nothing.
This very brief description of the MIX instruction set should give you an idea of the types of instructions which are available on the MIX machine, and the level of detail which is necessary when working in machine language. In fact, the level of detail needed to write programs in machine language is quite great, and in order to be able to program well for a computer it is necessary to understand the internal structure of the computer. The next chapter is a reference section which describes, in detail, the actual operation of the MIX computer.
Once you are familiar with the architecture and instruction set of the MIX computer, you can begin to program. In this section we present two ways to program: machine language and assembly language. These two programming languages are very similar and are often confused for each other. There is, however, a definite difference between the two, and almost no one voluntarily programs in machine language. After giving an example of machine language programming, we present the MIX assembly language, MIXAL, to provide the assembly language which is used in the remainder of this text.
Machine language is the only language which the MIX machine can execute: binary. Every instruction must be encoded in the proper numeric binary representation in order for the MIX computer to understand it. All computers can speak only machine language and, to make things worse, the machine language for most computers is different for each computer. The machine language is defined by the instruction set and instruction format of the computer.
For example, in MIX, the instruction to load the X register with the contents of location 1453 is, in binary
| +001100101011000000000101001111 |
| +1453000517 |
A program in machine language is a set of addresses of instructions and data and the contents of these memory locations. To illustrate machine language programming, let us write a machine language program for a very simple problem, such as adding two numbers and printing their sum.
Even solving this very simple problem requires careful thought. How are the two numbers to be input? What should the output look like? Where does our program go in memory? These questions are actually relatively minor, compared with the actual programming, and so they will be answered later. We will basically assume that the two numbers to be added are on an input card and the sum will be printed on the line printer. The general outline of our program is given by the following algorithm.
| Step I | Input the two numbers (IN) |
| Step II | Add the two numbers (ADD) |
| Step III | Output the sum (OUT) |
| Step IV | Stop (HLT) |
This is an algorithm for solving our problem, but it leaves a lot unsaid. In most higher level languages (such as Fortran, PL/I, Algol, and Pascal), each of the above steps could be expressed as a single statement in the higher-level language. In machine language, however, things are more difficult.
After each step of the above program, we have listed the (symbolic) opcode in MIX which will do roughly what we want. Upon careful examination, however, we find that these instructions are not quite sufficient. First, the IN and OUT instructions only start an I/O operation; the numbers will not be input or output until the device is not busy again. Also, both the card reader and line printer use a character code representation of data, while the ADD instruction must have its data in numeric binary. Thus, we must refine our statement of what is to be done in steps I and III, for the input and output. Our second version of a solution to this problem is, then,
| Step I | Input the two numbers | |
| I.1 | Begin reading the numbers (IN) | |
| I.2 | Wait until input complete (JBUS or JRED) | |
| I.3 | Convert the two numbers to binary from character code (NUM) | |
| Step II | Add the two numbers (ADD) | |
| Step III | Output the sum | |
| III.1 | Convert the sum to character code (CHAR) | |
| III.2 | Begin the output of the sum (OUT) | |
| III.3 | Wait until output complete (JRED or JBUS) | |
| Step IV | Stop (HLT) | |
When working with data in a computer, there are two properties of the data which must be kept in mind. One is the type of the data; that is, how it is represented. Data can be represented in many ways. The number 5, for example, can be represented as an integer number (+0000000005), as a floating point number (+4105000000), in character code (+3636363643), in character code for the Roman numeral representation (+3100000000), and so on. The same piece of data may exist in different representations at different times in the computer. For example, a CHAR instruction will convert a binary integer representation into a character code representation. Thus, the type of a piece of data is a dynamic property of the data; it may change with the execution of the program.
The other property which must be kept in mind when programming is the location of the data: where is it stored? Data may be stored in memory (which location?), in a register (which register?), or on an I/O device (which unit and where on that unit?). Data may exist in several places at the same time. After a LDA instruction, the data is in both the A register and in memory. Data may also exist in several different places, in different representations at the same time or at different times. It should be remembered that each piece of memory in a computer has one and only one value at any given time, so that two different items or two different representations of the same item cannot exist in the same location at the same time. The most common location for data is in one of the registers or in memory. Since the registers are needed for performing arithmetic, data is often kept in memory and loaded into a register only when needed.
But, to get back to the problem at hand, the algorithm above does not consider the problem of where our data is stored, or the effect of our operations upon these storage locations. We now should add whatever instructions are needed to put information in the right place for our instructions.
First, we note that the IN instruction will read our card into memory, while the NUM instruction wants its operands to be in the A and X register. Thus, our program for step 1.3 needs to be refined. We need to convert the first number, then the second number, from character code to numeric.
| I.3 | Convert the two numbers to binary from character code | |
| a. | Load first 5 bytes of character code of the first number into A register, second 5 bytes into X register (LDA, LDX) | |
| b. | Convert to numeric (NUM) | |
| c. | Store first number back into memory to free registers for next conversion (STA) | |
| d. | Load first 5 bytes of second number into A register, second 5 into X (LDA, LDX) | |
| e. | Convert to numeric (NUM) | |
| f. | Store second number in memory (STA) | |
| Step II | Add the two numbers | |
| II.1 | Load first number into A register (LDA) | |
| II.2 | Add second number (ADD) | |
| II.3 | Store sum back in memory (STA) | |
The conversion for output uses the CHAR instruction. This instruction assumes that its operand is in the A register and puts the character code representation of this number back into the A and X registers. The OUT for step III.2 assumes that the sum (in character code) is in memory. This means we need to refine III.1, as
| III.1 | Convert sum to character code | |
| a. | Load sum from memory (LDA) | |
| b. | Convert to character code (CHAR) | |
| c. | Store both A and X register into memory for output (STA, STX) | |
After these refinements, our entire algorithm looks like:
| Step I | Input the two numbers. | |||
| I.1 | Begin reading the numbers (IN) | |||
| I.2 | Wait until input complete (JBUS or JRED) | |||
| I.3 | Convert the two numbers to binary | |||
| a. | Load first number into A and X registers (LDA, LDX) | |||
| b. | Convert to numeric (NUM) | |||
| c. | Store first number (STA) | |||
| d. | Load next number into A and X (LDA, LDX) | |||
| e. | Convert to numeric (NUM) | |||
| f. | Store second number back in memory (STA) | |||
| Step II | Add the two numbers | |||
| II.1 | Load first number from memory (LDA) | |||
| II.2 | Add the second number (ADD) | |||
| II.3 | Store sum back in memory (STA) | |||
| Step III | Output the sum | |||
| III.1 | Convert sum to character code | |||
| a. | Load sum from memory (LDA) | |||
| b. | Convert to character code (CHAR) | |||
| c. | Store A and X registers for output (STA, STX) | |||
| III.2 | Begin the output of the sum (OUT) | |||
| III.3 | Wait until output is complete (JBUS or JRED) | |||
| Step IV | Stop (HLT) | |||
This gives us a complete set of instructions for our program. Looking them over, we should notice at once that some of the instructions are not needed. Specifically, the STA in step II.3 is followed by an LDA in step III.1a of the same information. Since the STA of step II.3 does not change the contents of the A register, we can drop the LDA altogether. As soon as we do this, we notice that the store in II.3 is now no longer needed either. Hence, we eliminate both the STA in II.3 and the LDA in III.1a.
Similarly, if we consider that addition is commutative (i.e., a + b = b + a), we realize that, since the NUM of step I.3e leaves its result in the A register and the ADD wants one of its operands in the A register, we can eliminate the STA in I.3f and the load in II.1, changing II.2 to adding the first number (from memory) to the second (in the A register).
These types of considerations are known as local optimizations, since we are improving the program (in terms of number of instructions, execution time, and number of data locations needed) by making only small changes in the program. These small changes only affect a small amount of the program, and take advantage of the local, temporary flow of data within the computer. This is in contrast to global optimization, which tries to improve the program by considering the entire program at once.
The next problem we need to face is: Where do we put our data? This is called storage allocation. It is necessary to use memory for our input, our output, and the temporary storage of the first number in memory. (Notice that our local optimization eliminated the need for memory to store either the second number or the sum.) For the input card, we will need 16 memory locations; the output line will require 24 memory locations. We need one location to store one of the numbers. If we start our program at location 0000 of memory, then we can allocate memory for our data either before or after our instructions. If we put our data before the program, then we can reserve locations 0000 to 0017 for the input card, 0020 for the number, and 0021 to 0050 for the output line image. Our instructions then begin at location 0051, and continue to (counting 16 instructions) 0070. Alternatively, we can put our 16 instructions at locations 0000 to 0017, our card image at 0020 to 0037, our first number at 0040, and our line image from 0041 to 0070. Since it makes no difference, we flip a coin, and it comes up, … tails! So we will put our data before our instructions.
Now, we can write what instruction goes into each memory location. We assume that the two numbers we are to add will be right-justified in columns 1 to 10 and 11 to 20 of the input card. We put the output sum in columns 1 to 10 of the line printer image.
| 0000-0017 | Card image | |
| 0020 | Storage location for one number | |
| 0021-0050 | Line printer line image | |
| 0051 | Begin input into locations 0000 to 0017 from card reader (IN) | |
| 0052 | Wait until the card reader is done by jumping to this instruction until card reader is not busy (JBUS) | |
| 0053 | Load first five columns of card from 0000 into A (LDA) | |
| 0054 | Load second five columns from 0001 into X (LDX) | |
| 0055 | Convert to numeric (NUM) | |
| 0056 | Store first number in 0020 (STA) | |
| 0057 | Load first five bytes of second number, columns 11-15, from location 0002 into A (LDA) | |
| 0060 | Load columns 16-20 from location 0003 into X (LDX) | |
| 0061 | Convert to number (NUM) | |
| 0062 | Add first number (in 0020) to A register (ADD) | |
| 0063 | Convert the sum (in A) to character code (CHAR) | |
| 0064 | Store first 5 bytes of sum in location 0021 (STA) | |
| 0065 | Store second 5 bytes of sum in location 0022 (STX) | |
| 0066 | Begin output of line image in locations 0021 to 0050 to line printer (OUT) | |
| 0067 | Wait until output is complete by jumping to this instruction until line printer is ready (JBUS) | |
| 0070 | Stop (HLT) |
Now that we have our program designed, we can convert this into machine language. This involves giving the (octal) machine language representation of each instruction. For the first one, we have an IN instruction, whose opcode is 44. The F field is the device which is the card reader, device number 16 (20 octal). The address field is the address of the first location to read into, in this case 0000. So our first instruction is
| 0051 | +0000 00 20 44 |
| 0052 | +0052 00 20 42 |
| 0051 | +0000 | 00 | 20 44 | Begin reading a card | ||
| 0052 | +0052 | 00 | 20 42 | Wait until read done | ||
| 0053 | +0000 | 00 | 05 10 | Put part of number in A | ||
| 0054 | +0001 | 00 | 05 17 | Put rest in X | ||
| 0055 | +0000 | 00 | 00 05 | Convert to numeric | ||
| 0056 | +0020 | 00 | 05 30 | Store for later ADD | ||
| 0057 | +0002 | 00 | 05 10 | Do the same for the | ||
| 0060 | +0003 | 00 | 05 17 | Second number | ||
| 0061 | +0000 | 00 | 00 05 | Convert to numeric | ||
| 0062 | +0020 | 00 | 05 01 | Add the two numbers | ||
| 0063 | +0000 | 00 | 01 05 | Convert sum to characters | ||
| 0064 | +0021 | 00 | 05 30 | Store first 5 characters | ||
| 0065 | +0022 | 00 | 05 37 | And second 5 characters | ||
| 0066 | +0021 | 00 | 22 45 | Start print of sum | ||
| 0067 | +0067 | 00 | 22 42 | Wait until print is done | ||
| 0070 | +0000 | 00 | 02 05 | Stop |
Machine language is hardly worth the effort, however. Any little change would require us to rewrite the entire program. To add an instruction to test for overflow, for example, requires inserting a JOV instruction right after the ADD instruction at location 0011. This would require all the addresses of instructions and data which follow the ADD to be increased by one, and result in changing many of the address fields in the program. Also the last step of actually converting our program into machine language was very simple from an intellectual point of view, but dull, monotonous, and error prone. (I made at least five errors in the first translation into machine code for this example.)
These problems, among others, make it very difficult to program in machine language. However, machine language is very powerful, in the sense that if the computer can possibly do a certain thing, it can be done in machine language simply by creating the correct instruction or instruction sequence. Assembly language is a computer programming language which allows the programmer to exercise total control over the computer, as can be done in machine language, but also relieves the programmer of some of the hassles of machine language.
One of these hassles is the final translation of the program from a descriptive (but detailed) statement of the program into the actual numeric binary machine language. Notice that our writing of the machine language program was divided into two steps. The first was the creative one, deciding what the steps of the solution would be, which instructions to use, where to allocate space for data and where to allocate space for the instructions, considering the type and location of the data.
The second step was the relatively trivial, mechanical process of translating the program which resulted from the first step into machine language. This translation step requires no creativity, only the ability to derive, from our description of the program, the four fields of each instruction and assemble them into one machine language statement. The only difficult part is determining from our description what the four fields (opcode, field, index and address) of the instruction should be. If we would accept writing this description in a special format -- one that explicitly states each field -- then the actual construction of each instruction would be very easy and could even be done by a computer. This is the basic idea behind an assembler.
An assembler is a computer program which translates from assembly language into machine language. Assembly language is a simple way of describing instructions for a machine language program which is more convenient than machine language. The assembler reads these descriptions and translates them into a machine language instruction. After this translation, called assembly, is complete, the resulting machine language program can be executed by the computer.
The assembler needs one assembly language statement for each machine language statement. For MIX, we must specify four fields for each instruction:
| opcode | address, index(field) |
| Bytes | 0 | 1 | 2 | 3 | 4 | 5 |
| address | index | field | opcode | |||
This is some help, but the assembler does more. Each of the fields is, in machine language, a binary number, and the assembly language must specify what these numbers are. People, and programmers, have difficulty working with numbers all the time, however, and are more comfortable with symbolic, word-like quantities. Thus, assembly language uses symbolic opcodes to specify the opcode of an instruction. The assembler has a table which gives, for each symbolic opcode, the corresponding numeric opcode. This allows the assembly language programmer to write
| +1453 | 00 | 05 | 33 |
Another convenience provided by the assembler is the ability to express the address field of the instruction by a symbolic name, rather than an actual number. In our example of the last section, we had three data items: the number stored in memory, the input card, and the output line. Rather than giving numeric addresses for each of these, we can use a symbolic name (such as FIRSTNUM, CARD, LINE) to represent the numeric address and have the assembler automatically substitute the numeric address for the symbolic address during assembly. This allows us to write an assembly language statement like
Several other conveniences can be provided by the assembler. For most of our instructions, the index field will be 00 and the field specification will be 05. Rather than having to specify these fields for each instruction, the assembler allows these fields to not be specified; they are optional. If the contents of a field are not specified, its default value (00 for the index field and 05 for most field specifications) is used.
Another convenience is in the specification of numbers. Rather than requiring numbers to be specified in binary or octal, the assembler expects numbers to be written in decimal, and will convert these decimal numbers to binary for the programmer. This relieves the programmer of the burden of converting numbers (which are thought of in decimal) into octal for the program, but has the contrary result of requiring that numbers thought of in octal must be converted to decimal for the assembler (which then converts them back into octal for the machine language program).
There are many other properties of assemblers, and each assembler will be different from each other assembler in some way. This is because different computers have different instruction sets and instruction formats. Also, it is because assemblers are programs, written by programmers, and hence reflect how the writer of the assembler views how things should be done. Assembly language is defined by the assembler and may thus be full of arbitrary decisions. It is necessary to write programs in the conventions defined by the assembly language only if you want to use that assembler. If you do not want to write programs in the way that the assembler says they must be written, you should feel free to write in machine language, write your own assembler, or use some other assembler. Some computers do have several assemblers.
In this text, from now on, we use the MIX assembly language, MIXAL. We give now a definition of that language.
The MIX assembler reads assembly language programs, normally prepared on punched cards, and produces a numeric machine language program and a listing of the input program. The listing is printed on a line printer and consists of the assembled machine language program and the original assembly language program. Each line of the output listing corresponds to one input card image.
An assembly language program is made up of a sequence of assembly language statements. Each statement is one card or line image. There are two types of statements: comments and non-comments. If a MIXAL statement has an "*" in column 1 of the input card, it is a comment card. Comment cards are not used by the assembler to generate an instruction in the machine language program, but should be included by the assembly language programmer to describe, for himself and future programmers, what the program is doing and how. Comment cards are copied to the output listing of the program but have no other effect on the assembler.
Noncomment cards are all statements without an "*" in column 1. These are the statements which result in machine language instructions. These cards are prepared in an assembly language statement format. This format consists of four fields in the following order.
After the label field is the opcode field. This field contains the symbolic opcode for the machine language instruction to be assembled. The symbolic opcodes which are used in MIXAL are listed in Appendixes B, C, and D.
The next field is the operand field. The operand field specifies the operand for the instruction. For most instructions (the memory reference instructions), this consists of three (optional) subfields: the address field, the indexing field, and the partial field specification. For immediate instructions, the operand field specifies the operand and any indexing. (The contents of byte 4 of the machine language instruction, the opcode modifier, is not a partial field specification, but identifies which of the immediate instructions is given.) The form of this field will be considered in more detail below.
The last of the four fields is the comment field. This field allows each and every statement in an assembly language program to be commented, this field should be used often, in a descriptive way, to aid the reader of a program to understand what a program is doing and how this particular instruction is being used to help the program work. Comments are very important to good programs, and particularly to assembly language programs.
The placement of the fields in an assembly language on an input card can be done in two general ways: fixed-format and free-format. A fixed-format assembler requires that each field be contained within specific columns of the input card. Some MIXAL assemblers are fixed-format, and for these assemblers, the input format is:
| Columns | Field | Comments | |
|---|---|---|---|
| 1-10 | Label | If a label is given, it must be left-justified, with blank fill (i.e., the symbol starts in column 1 and continues for as many columns as necessary, but no more than 10. The rest of the field is left blank). | |
| 12-15 | Opcode | Each symbolic opcode has been defined so that it is 3 or 4 characters long, so no more than 4 columns are needed. | |
| 17-? | Operand | Starts in column 17 and continues for as many columns as needed, but not beyond column 80. This field is terminated by the first blank column. | |
| ?-80 | Comment | Follows the operand field and is separated from it by at least one blank; continues to the end of the card. |
Column 11 (between the label and the opcode field) and column 16 (between the opcode and operand field) are left blank to improve the readability of the program, by insuring at least one blank between each field.
Notice how the comment field cannot be defined to occupy only certain columns, the way the label and opcode fields can. This is because the operand field may be of varying complexity and length. Normally, the operand field will be less than twenty columns in length, so one can almost always assign columns 17-36 for the operand and 38-80 for the comment field. Occasionally the operand may be longer, but most of the time it is shorter. Thus, the operand field is not terminated by a specific column but by the first occurrence of a blank, with the comment field being able to begin immediately after the delimiting blank. This idea can also be applied to the other fields of the statement, and is the basis of free-format input.
Since a blank cannot be a part of a symbol or a number, it can be used as a delimiter. For free-format input, the fields are separated by one or more blanks and are not constrained to begin in any specific set of columns. The label field starts in column 1, and ends with the first blank. The opcode field begins with the next non-blank character and is terminated by the first following blank. The operand field begins with the next non-blank and is terminated by the next blank; the rest of the card is the comment field. The label field is optional. If it is not present, the delimiting blank must still be included, so a blank in column 1 specifies that the label field is not present (or is blank). If column 1 is non-blank, then either it is a comment (* in column 1) or a label (symbol begins in column 1 and continues until the first blank).
Free-format input is almost always easier to prepare than fixed-format input, while it is easier for the assembler to input only fixed-format. Your assembler may be either. Notice, though, that a free-format assembler can accept programs which have been prepared in a fixed format, but not generally vice versa. Also, fixed-format input produces a listing which is attractively laid out in columns. Thus, most assembly language programs are prepared in fixed-format. The use of a program drum on a keypunch or the tab mechanism of a typewriter or computer terminal can make it quite easy to prepare fixed-format assembly language programs.
The major advantage of using an assembly language is the ability to use symbolic names rather than numeric constants. Two types of symbols are used: symbolic opcodes (defined by the assembler) and symbols defined by the user. The assembler has a table of each kind of symbol. The table contains, at least, the name of the symbol and its value. When the assembler is examining the opcode field of a statement, it searches the opcode table. If a symbolic opcode is found in the table which is equal to the symbolic opcode of the assembly language statement, then the value associated with that symbolic opcode is the numeric opcode and standard field specification for the assembled machine language statement.
Similarly, another table contains the user defined symbols and their (user-defined) values. The value of a symbol is normally an address. As the assembler reads the program, and translates it, card by card, into a machine language program, new symbols may be defined and put into this symbol table, along with their values. Then if a symbol is used, later in the program, the symbol table is searched and the value of that symbol is used where the symbol occurs. Symbols may be defined only once, and so always have the same value once they are defined.
| Symbols | Values | |
|---|---|---|
| ABCD | 437 | |
| TR1 | -1 | |
| 5XY7KD3 | 263 | |
| ONE | 100005 | |
| NOW | 0 |
There are two ways to define symbols, with the EQU statement (which we will discuss later) and with the label field of an instruction. Since most symbols are symbolic addresses, they are used as the label for the location whose address is their value. Remember that each instruction in a machine language program goes in a specific memory location. To specify an instruction, it is necessary to give both its address and its numeric machine language representation. Most programs are placed in consecutive locations in memory, one after another. To minimize the need for the programmer to specify the address of every instruction, the assembler uses a special variable called the location counter to determine the address into which each assembled instruction should be put. After an instruction is assembled and printed on the output listing, the assembler reads in another card, and increments the location counter by one. It assembles that card, prints it, reads in the next one, increments its location counter, and so on, until the end of the assembly program is reached. The location counter is a variable in the assembler whose value is the address at which the current assembly language instruction is to be placed in memory. When a label is encountered on an assembly language statement, the symbol which is the label is entered into the symbol table with a value which is the current value of the location counter; that is, the address of the labelled instruction. As an example, consider the following sequence of instructions
The major use of symbols is in the specification of the operand field of a MIXAL instruction. The operand field is composed of three fields: the address field, the index field, and the field specification. The contents of these fields can be specified in very general ways, but it is best to keep in mind that the resulting value for each subfield must be an integer number which is in the correct range for the part of the MIX instruction which it specifies. Thus, the address part must be in the range -4095 to +4095, and the index and field specification values must be in the range 0 to 63.
The basic components for specifying the operand of an instruction are of two types: numbers and symbols. A number can be considered a self-defining symbol, in that its value is represented by itself. All numbers are interpreted as decimal integers and must be less than the maximum integer which a MIX word can represent. When a number is used in an operand, the assembled instruction will use that number. The other basic component is a symbol. The value of a symbol is the value which has been stored in the symbol table for that symbol.
In addition to these two types of values, numbers and programmer-defined symbols -- one other symbol can be used in operand field specifications. This is the symbol "*". * (pronounced star) has as its value the value of the location counter, the address of the instruction currently being assembled. This is useful in such situations as waiting for a device to finish an I/O operation, as in
Any of these three (number, symbol, or *) may be used for the operand field of an assembly language statement. In addition to being used singly, they may be combined in expressions. An expression is any number of numbers, symbols, or *s, combined by any of the five binary operators +, -, *, /, :, with an optional leading plus or minus sign. The value of the expression is determined from the value of its components. The value of a number is that number; of a symbol, the value stored in the symbol table; and of *, the address of the current instruction. If these are combined by operators, the evaluation of the expressions "a + b", "a - b", "a * b", and "a / b", is the normal result of addition, subtraction, multiplication and (integer) division, on the MIX machine. The result of any expression evaluation may not exceed five bytes plus sign. The expression a:b is evaluated as (8 × a) + b. This is used mainly for specifying the contents of index fields and partial field specifications, but may be used more generally. (Notice that if a and b are 0 ≤ a, b ≤ 7, then a:b is the octal number whose "eights" digit is a and whose units digit is b).
The evaluation of expressions is strictly left to right. No parenthesis can be used to group subexpression evaluation and no operator has precedence over another. Thus, the expression
1+2-3*4/5is evaluated as
((((1 + 2) - 3) × 4) / 5) = 0and 2*4-2*4 = 24. Strictly left to right.
Examples:
4+5 equals 9 3+5*6 equals 48 7+2:6 equals 78 7+2:6+1 equals 79
Each subfield of the operand field of an assembly language statement may be an expression (with the constraint that the resulting value must be in the proper range). Each field may also be absent. The form of the operand field is "address,index(field)". If a particular subfield is absent, then its delimiter is also. Thus, if the index field is missing, zero is assumed and the comma separating the address and index fields is not present. If the field specification is missing, then the default is the standard field setting (0:5 for all memory reference instructions except STJ, for which it is 0:2). If the address is missing, it is assumed to be zero.
The assembly process can now be described in considerable detail. It will be examined in more detail in Chapter 8, but a brief walk-through of the assembly process here will make it easier to understand assembly language programming. Each card is handled separately. First, a card is read. If column 1 is a "*", the card is copied to the printer, and we have completed this card and may start the next. For a non-comment card, the label field is examined. If it is non-blank, the symbol in the label field is entered into the symbol table with a value of the location counter. Next, the opcode is translated into its numeric form for byte (5:5) of the machine language instruction and the standard field setting defined for byte (4:4). The operand field expressions are evaluated, looking symbols up in the symbol table and using the value of the location counter for *, as needed. This specifies bytes (0:2), (3:3), and sometimes (4:4) of the instruction. All of these are assembled to form the machine language instruction which is output. The input assembly statement and the assembled machine language instruction are also printed on the line printer. Then the assembler increments the location counter, reads the next card, and repeats this entire process for the next card.
Several points still need to be considered. At several places in the assembler, errors can occur. Most of these are treated in a reasonable way. If a symbol is defined in the label field of a statement, and that symbol already exists in the symbol table, then the symbol is doubly defined, or more generally, multiply defined. The second definition is ignored and the output line is flagged to indicate the error. If the opcode cannot be found in the opcode table, it is an undefined opcode or an illegal opcode and is treated as a NOP instruction. If the operand field, or any of its subfields, is botched (by two operators next to each other, undefined symbols, results too large for the field, or results which exceed 5 bytes plus sign in an intermediate step), the default values are normally used. In all cases, the statement is flagged on the output listing and often the machine language program will not be executed.
One special case comes up in evaluating the address subfield of the operand. Suppose we wish to write the following
A number of questions can still be raised concerning the assembler operation. How does it stop? What is the initial value of the location counter? How are data values specified? These and other questions reveal the need to be able to give the assembler information other than simply the assembly language statements which are to be converted into machine language instructions. This control information could be specified in several ways, but for esthetic reasons it is felt to be nice if all input to the assembler has (roughly) the same format. Thus, a number of assembly instructions have been defined which resemble in their appearance the format of the machine instructions given above. These assembler instructions are not machine operations, so their symbolic notation cannot be called opcodes. However, their resemblance to opcodes has resulted in their being called pseudo-instructions. The MIXAL language has five pseudo-instructions: ORIG, CON, ALF, EQU, and END. The treatment of each of these is quite different from the treatment of the machine opcodes, and so we discuss each in some detail.
The placement of machine language instructions in memory is controlled by the value of the location counter, . The location counter starts initially at zero, 0000, at the very beginning of the program and is normally increased by one after each machine language statement is generated. Occasionally, it is necessary to reset the location counter to another value. For example, if we wish our program to be placed in memory starting at location 3000, rather than at 0000. This can be accomplished by the ORIG pseudo-instruction. The format of the ORIG statement is
The symbol P will have the value 1000, the symbol Q will have the value 2000 and the symbol R will have the value 2001.
This statement can be used to reserve memory locations whose initial value is not important. For example
The first ORIG sets the location counter to 2140. The label ARRAY is entered into the symbol table and given a value before the second ORIG takes effect, so its value will be 2140. For the second ORIG, the evaluation of the expression is * (whose current value is 2140) plus 20, or 2160, so the location counter * is reset to be 2160. The LDA then is assembled into location 2160, leaving 20 empty memory locations, addressable as ARRAY, ARRAY+1, ARRAY+2, …, ARRAY+19.
A program is made up of two parts: instructions and data. We have already seen how instructions may be specified by using a symbolic opcode and expression. What about data? The ORIG statement can be used, as illustrated above, to reserve memory space for variables whose initial value is not important, but, sometimes, the initial value is important. For example, if we are running an index register, say 15, in a loop from 1 to 16, we need to be able to compare the contents of 15 with 16. There is no immediate compare instruction, so it is necessary to create a memory location someplace whose contents are 16. If we give this the label SIXTEEN, we can then write
[label] CON w-value [comments]The label, if present, is assigned the value of the address of the location counter. In this location will be put one word, then the location counter will be incremented for the next instruction and the next card read and assembled. The contents of the word are specified by the w-value. A w-value is used to describe a full-word MIX constant. In the simplest case, this is just an expression and the expression is put into the word which is assembled. However, we may want to define specific values for specific bytes or fields of the constant being assembled. As an example, suppose we wish to store two numbers in one MIX word, one number in bytes (1:2) and the other in bytes (4:5). If we want to put 17 into bytes (4:5) and 43 into bytes (1:2), we can write
In general the form of a w-value is
| expr1(field1), expr2(field2), …, exprk(fieldk) |
The word which results is the result of taking a zero word of MIX memory and placing the value of expr1 in field1 then the value of expr2 in field2, then …, and finally the value of exprk in fieldk. All expressions (and field expressions) must be evaluatable; that is, no forward references are allowed. Any field in the MIX word which is not set by any field will be zero; the sign bit will be "+" if not otherwise specified. If a field specification is absent, (0:5) is assumed. If an expression is absent, it is assumed zero. Remember that the evaluation of expressions and storage in fields is strictly left to right, so if the partial fields overlap, the rightmost one will be used. Thus, the result of
| + | 00 | 00 | 01 | 00 | 27 |
The CON pseudo-instruction affects only the initial value of the location defined by it. If we define
In addition to wanting to define numeric constants, it is sometimes necessary to define alphanumeric character code constants. This is accomplished by the ALF instruction. Each word in MIX memory is made up of five bytes and each byte can hold one character. The ALF pseudo-instruction takes as its operand five characters and assembles one word whose contents will be the character code for these five characters. For example
| Statement | Resulting MIX word | |
|---|---|---|
| ALF ABODE | +0102030405 | |
| ALF MIXAL | +1611330115 | |
| ALF 12345 | +3740414243 |
The format of the ALF statement is
[label] ALF 5 characters [comments]The label, if present, is given a value of the address of this word.
For a fixed-format assembler, the five characters are the contents of columns 17-21 of the input card. For a free-format assembler, however, it is not so easy. In a free-format assembler, the fields are separated by one or more blanks, because for all instructions (except ALF) blanks are not important and cannot appear within a symbol or expression. For the ALF instruction, blanks can be very important. Suppose we want to construct two alphabetic constants, one of an A followed by four blanks, the other of one blank, then an A, followed by three blanks. In a free-format assembler, the leading blank of the second constant would be thought to be part of the delimiting blanks between the ALF pseudo-instruction and its operand string, and hence it would be ignored, unless ALF is treated specially. This problem is common to other assemblers and can be solved in several ways. The simplest is to state that the ALF pseudo-instruction is always followed by exactly two blanks and then the five characters to be put in the MIX word. (Two blanks allows the operand to start in the same column as everything else if a fixed-format is being used.) Thus, to create the two constants mentioned above we would write (where we are using a "." to represent a blank in order to emphasize the spacing)
Another approach is to introduce a special delimiter which is used to surround and delimit the five characters which are to be used for the ALF. For example, if a quote is the delimiter, then the two above constants are
Other variations are also possible. The specific method used by your assembler may vary from those presented here. The ALF pseudo-instruction is one reason why a fixed-format input is often used; it avoids these problems.
We have already seen that one way to define a symbol is to place it in the label field of an instruction. The symbol so defined then has a value which is the address of the memory location for which that instruction is assembled. There are other times, however, when we wish to use symbols whose values do not correspond to memory addresses. These values may be device numbers (16 for the card reader; 18 for the line printer), lengths of tables or arrays, special values for flags or switches, or any of a number of other purposes. The EQU pseudo-instruction is a means of defining a symbol and putting it in the symbol table without affecting the location counter or assembling any code. The format of the EQU pseudo-instruction is
[label] EQU w-value [comments]If the label field is non-blank (it really does not make sense for it to be blank), the w-value in the operand field is evaluated to give a five-byte-plus-sign value. Then the symbol in the label field is entered into the symbol table with a value of the evaluated w-value. The w-value cannot have any forward references. The value of the location counter is unchanged. No machine language instruction is generated.
Examples:
Appropriately enough, the last pseudo-instruction is the END pseudo-instruction. The END pseudo-instruction signals to the assembler that the last assembly language statement has been read, and the program is now completely input. The assembler then terminates its operation, having completed the translation of the assembly language program into a machine language program. The format of the END statement is
[label] END [w-value] [comments]If a label is given on the END card, it is given a value of the address of the first location beyond the end of the program. Thus, if the program ends with
If an operand (the w-value) is given on the END card, it is taken to be the address where execution of the program should begin. If no operand is given, the program will be started at location 0000.
If there are any undefined symbols in the program (i.e., forward references which never did appear as labels), the assembler will define them as CON 0 statements occurring just before the END card. Undefined symbols are generally considered programming errors and should be avoided, but if you do forget some, the assembler will assume that you meant to define them as the label of a CON 0 at the end of your program.
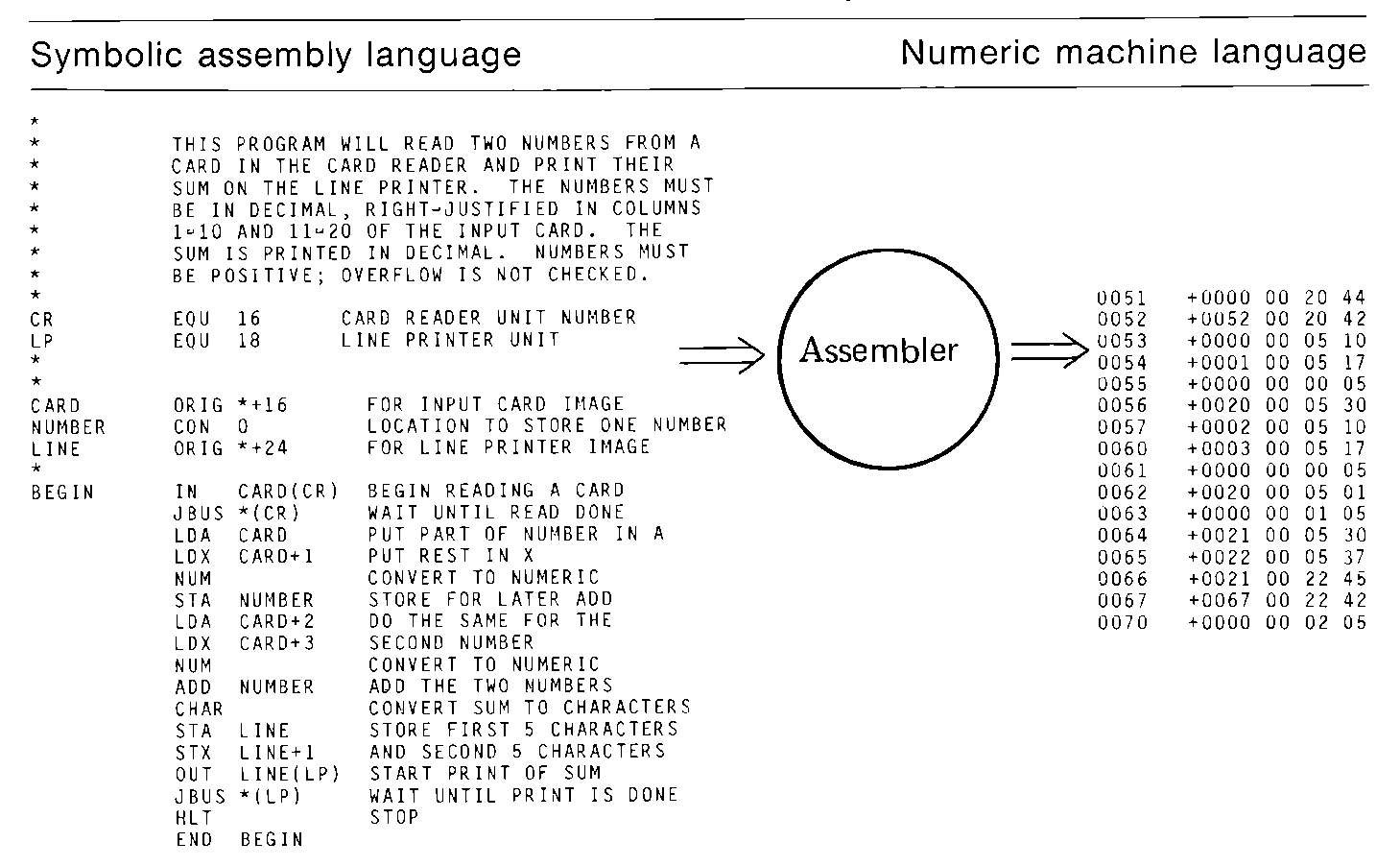
As an example, we present the assembly language program which is equivalent to the machine language program presented in Section 2.2. This program reads two numbers from the card reader and prints their sum on the line printer. The assembler translates the following assembly language program into the machine language program of Section 2.2.
Many of the features of assembly language are provided to make programming more convenient. The ability to use symbolic opcodes and operands, to specify numbers in decimal, and other features are both a convenience, and to some degree, necessary to make assembly language programming a reasonable task. In this section we discuss two more features of MIXAL which are convenient, but not as necessary; they simply make programming easier by allowing us to program in terms which are closer to the way in which we think of the programming task.
When we are programming, it is sometimes necessary to refer to a constant value which should be stored somewhere in memory. For example, if we have an index register, say 4, which is controlling the number of times that a loop is executed by ranging from 1 to 24, we would want to compare the register against the constant 24. We could do this by writing
The assembler, when it finds a literal, stores it in the symbol table as a forward referenced symbol. When the END card is read, the symbol table is searched both for undefined symbols (as explained above) which are defined as CON 0 statements just before the END statement, and for literals. All literals are also defined as memory locations just before the END card. The contents of the memory location is the value of the w-value which defined the literal. If the literal symbol is =w=, this will result in the generation of an assembly language statement
Literals are quite useful, since they allow the reader of an assembly language program to see at once both the instruction and the contents of the literal, instead of seeing a label and having to search throughout the program for that label to discover the contents of the location. Literals also help avoid accidentally forgetting to define symbols with a resultant CON 0 being generated instead.
Examples:
A second convenience in MIXAL is local symbols. For all loops or jumps, it is necessary to use a label in order to have an address to jump to. For short loops or branches this may result in a large number of labels, each of which must be unique. Normally, the label should be picked to reflect the meaning of the code which it labels, but often it becomes difficult to think of unique names which may describe code which is basically the same except for subtle differences. To solve this, MIXAL provides local symbols. Local symbols are the 10 symbols 0H, 1H, 2H, …, 9H. They are referenced by the symbols 0F, 1F, 2F, …, 9F when the local symbol is a forward reference, and by 0B, 1B, 2B, …, 9B when the local symbol is a backward reference. The H stands for "Here," the F for "Forward," and the B for "Back." The digit is used to allow 10 different local symbols. When a reference to iB is encountered (for i = 0, 1, …, 9), the assembler uses as the value of the local symbol the value of the most recently encountered iH symbol; when a reference to iF is encountered, the assembler treats it as a forward reference to the next iH symbol it finds. Because of this convention, the iH local symbols may be used many times in a program without resulting in multiply defined symbols. For example
The MIX computer is a small, general purpose computer whose architecture was defined by Knuth (1968). In this chapter, we first briefly described the architecture of the MIX computer, and then we presented an example of how machine language programs are written, showing the difficulty of programming in machine language.
An assembler is a program which translates from assembly language into machine language. With the exception of the assembler pseudo-instructions of ORIG, EQU, and END, each and every assembly language statement results in one machine language instruction or data value. The assembly language statement is composed of several fields in either a fixed-format or a free-format. The label field defines a symbol which may be used as the operand of other statements to reference the labelled instruction. The opcode and operand fields specify the machine language opcode, indexing, field specification, and address fields for the assembled instruction.
The assembler pseudo-instructions allow the location counter for assembly to be set (ORIG), numerical constants (CON) or alphanumeric character code constants (ALF) to be defined, symbols entered into the symbol table with a value other than an address (EQU), and define the end of the assembly program (END). Literals and local symbols make assembly language programming easier.
MIXAL was defined by Knuth (1968). However, each MIX computer system will have its own MIXAL assembler. This means that the operation and some of the specifics of your MIXAL assembler may differ from the assembler described here or in Knuth (1968). Check with your instructor for a manual or report describing your specific MIXAL assembler and its use.
Chapter 3 describes the MIX computer in more detail.